In the previous section we learned the method to compare any given fractions. But there are some special cases where we will not have to do any calculations on paper. We will be able to do some 'mental calculations' and say which of the given fractions is the largest or smallest.
Consider the situation in which we are given some like fractions. We are asked to pick the largest among them. We can proceed as follows:
• We know that the like fractions have the same denominators. So in all the fractions, the 'whole' is divided into the 'same number of equal parts'.
• So with out any calculations, we can say that the fraction with the largest numerator is the largest fraction. And that with the smallest numerator is the smallest fraction. We can even arrange the given fractions in ascending or descending order.
Example: Given 4/15, 12/15, 2/15, 7/15.
In each of the above fractions, the 'whole' is divided into 15 equal parts. The quantity that we get depends on the number of pieces that we take. The number of pieces taken is indicated by the numerator.
So 12/15, with the largest numerator will be the largest fraction.
If we arrange them in ascending order, the list will be as: 2/15, 4/15, 7/15, 12/15
Another situation where we can do the calculations mentally, is when the numerators are all equal. The denominators can be different.
Example: 4/12, 4/17, 4/9, 4/21
Let us see how the calculations are done in this case:
• When the denominator increases, it means that the number of equal parts into which the 'whole' is divided also increases
• When the number of equal pieces increases, the size of each piece decreases. So 1/17 will be less than 1/12.
• It follows that '4 pieces of 1/17 each' which is 4/17, will be less than '4 pieces of 1/12 each' which is
4/12
• Thus it follows that when the numerators are all same, the fraction with the smallest denominator will be the 'largest fraction'
• So in the above example, 4/9 is the largest.
• If we arrange them in ascending order, the list will be as: 4/21, 4/17, 4/12, 4/9
We will now see some solved examples based on the above discussion:
Solved example 5.19
Show the following fractions on a number line:
4/8, 3/8, 6/8, 1/8, 8/8
Solution: In the following fig.5.23, the distance between 0 to 1 is divided into 8 equal parts. The required fractions are marked clearly.
Solved example 5.20
Put appropriate signs '<' or '>' in the boxes:
Solution:
(a) • 7/12 and 5/12 are like fractions. Because their denominators are the same. So both of them represent a fraction of a 'whole' which is divided into 12 equal parts.
• The value will depend on the number of parts taken out from the 12 equal parts.
• 7 > 5. So 7/12 > 5/12
(b) • From the number line of the previous solved example 5.18, we can see that, 0 lies at the extreme left end.
• This means, no part (ie., zero part) is taken out from the equal divisions.
• But in the case of 3/8, three parts are taken out.
• Obviously 3 > 0. Thus 3/8 > 0
In this way,the rest of the problems can be solved easily:
(c) 8/15 < 12/15 (d) 1/8 < 8/8
Solved example 5.21
Put appropriate signs '<' or '>' between the following pairs of fractions using 'mental calculations'. For each of them, prove the answer by drawing figures.
(a) 3/7, 3/9 (b) 4/11, 4/6 (c) 6/12, 6/7
Solution:
(a) The numerators are equal. So we can use the method that we discussed in the first part of this section above. That is., the fraction with the smallest denominator will be the largest. So we can write: 3/7 > 3/9. Proof:
In the first number line, the distance from 0 to 1 is divided into 7 equal parts. In the second, the same distance is divided into 9 equal parts. We can see that 3/7 is larger than 3/9
(b) 4/11 < 4/6. Proof:
(c) 6/12 < 6/7. Proof:
With this, we have completed all types of problems in the topic 'Comparison of fractions'. In the next section we will discuss about Addition of fractions.
Consider the situation in which we are given some like fractions. We are asked to pick the largest among them. We can proceed as follows:
• We know that the like fractions have the same denominators. So in all the fractions, the 'whole' is divided into the 'same number of equal parts'.
• So with out any calculations, we can say that the fraction with the largest numerator is the largest fraction. And that with the smallest numerator is the smallest fraction. We can even arrange the given fractions in ascending or descending order.
Example: Given 4/15, 12/15, 2/15, 7/15.
In each of the above fractions, the 'whole' is divided into 15 equal parts. The quantity that we get depends on the number of pieces that we take. The number of pieces taken is indicated by the numerator.
So 12/15, with the largest numerator will be the largest fraction.
If we arrange them in ascending order, the list will be as: 2/15, 4/15, 7/15, 12/15
Another situation where we can do the calculations mentally, is when the numerators are all equal. The denominators can be different.
Example: 4/12, 4/17, 4/9, 4/21
Let us see how the calculations are done in this case:
• When the denominator increases, it means that the number of equal parts into which the 'whole' is divided also increases
• When the number of equal pieces increases, the size of each piece decreases. So 1/17 will be less than 1/12.
• It follows that '4 pieces of 1/17 each' which is 4/17, will be less than '4 pieces of 1/12 each' which is
4/12
• Thus it follows that when the numerators are all same, the fraction with the smallest denominator will be the 'largest fraction'
• So in the above example, 4/9 is the largest.
• If we arrange them in ascending order, the list will be as: 4/21, 4/17, 4/12, 4/9
We will now see some solved examples based on the above discussion:
Solved example 5.19
Show the following fractions on a number line:
4/8, 3/8, 6/8, 1/8, 8/8
Solution: In the following fig.5.23, the distance between 0 to 1 is divided into 8 equal parts. The required fractions are marked clearly.
 |
| Fig.5.23 |
Put appropriate signs '<' or '>' in the boxes:
Solution:
(a) • 7/12 and 5/12 are like fractions. Because their denominators are the same. So both of them represent a fraction of a 'whole' which is divided into 12 equal parts.
• The value will depend on the number of parts taken out from the 12 equal parts.
• 7 > 5. So 7/12 > 5/12
(b) • From the number line of the previous solved example 5.18, we can see that, 0 lies at the extreme left end.
• This means, no part (ie., zero part) is taken out from the equal divisions.
• But in the case of 3/8, three parts are taken out.
• Obviously 3 > 0. Thus 3/8 > 0
In this way,the rest of the problems can be solved easily:
(c) 8/15 < 12/15 (d) 1/8 < 8/8
Solved example 5.21
Put appropriate signs '<' or '>' between the following pairs of fractions using 'mental calculations'. For each of them, prove the answer by drawing figures.
(a) 3/7, 3/9 (b) 4/11, 4/6 (c) 6/12, 6/7
Solution:
(a) The numerators are equal. So we can use the method that we discussed in the first part of this section above. That is., the fraction with the smallest denominator will be the largest. So we can write: 3/7 > 3/9. Proof:
 |
| Fig.5.24 |
In the first number line, the distance from 0 to 1 is divided into 7 equal parts. In the second, the same distance is divided into 9 equal parts. We can see that 3/7 is larger than 3/9
(b) 4/11 < 4/6. Proof:
 |
| Fig.5.25 |
(c) 6/12 < 6/7. Proof:
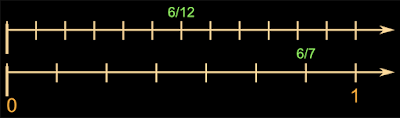 |
| Fig.5.26 |
With this, we have completed all types of problems in the topic 'Comparison of fractions'. In the next section we will discuss about Addition of fractions.

No comments:
Post a Comment