Chapter 37.7 - Ogive curves - Solved examples

In the previous section we saw ogive curves. We saw some examples too. In this section we will see some solved examples.
Solved example 37.15
The following distribution gives the daily income of 50 workers of a factory.

Table.37.55

Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Solution:
1. To draw the less than ogive:
• We want the the upper limit of each class interval to use as the x coordinates
• We want the corresponding values in the 'less than' cumulative frequency column to be used as the y coordinates
• So x coordinates are already available in the question. The y coordinates are tabulated in the third column of the table 37.56 below:

Table.37.56

2. So the coordinates are:
(120,12), (140,26), (160,34), (180,40), (200,50)
• The required ogive is shown in fig.37.8 below:

Fig.37.8

• Note that a kink is given in the x axis between O and 110. This is because, the values between (0,0) and (110,0) are not required for this problem

Solved example 37.16
During the medical check-up of 35 students of a class, their weights were recorded as follows:

Table.37.57

Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify the result by using the formula.
Solution:
1. To draw the less than ogive:
• We want the the upper limit of each class interval to use as the x coordinates
• We want the corresponding values in the 'less than' cumulative frequency column to be used as the y coordinates
• So y coordinates are already available in the question. They are shown again in the third column of table 37.58 below.
The x coordinates can be obtained from the class intervals tabulated in the first column of the table 37.58 below:

Table.37.58

2. So the coordinates are:
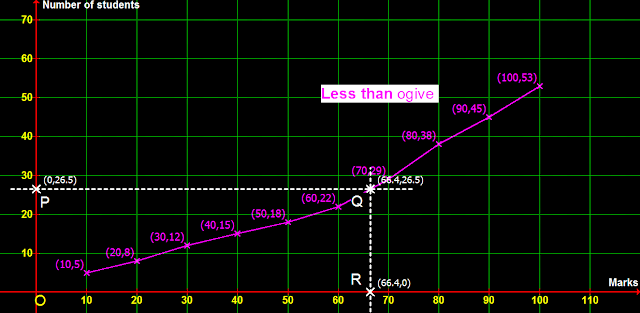
(38,0), (40,3), (42,5), (44,9), (46,14), (48,28), (50,32), (52,35)
• The required ogive is shown in fig.37.9 below:

Fig.37.9

2. Calculation of median from the ogive:
(i) Mark P on the y axis such that, the y coordinate of P is (ⁿ⁄₂) = (³⁵⁄₂) = 17.5
(ii) Draw a horizontal dashed line through P. Let it meet the ogive at Q
(iii) Draw a vertical dashed line through Q. Let it meet the x axis at R
• The coordinates of R are: (46.5,0)
• So median = 46.5 kg
3. Now we will check the median using the formula:
• In this problem, the total number of observations 'n' = 35. So ⁿ⁄₂ = ³⁵⁄₂ = 17.5
• The cumulative frequency closest to and just greater than 17.5 is 28
• The class corresponding to the cumulative frequency 28 is 46-48
• So 46-48 is the median class. It's frequency = 14
■ The median is calculated using the following formula:

Where:
l = lower limit of the median class = 46
n = number of observations = 35
cf = cumulative frequency of the class preceding the median class = 14
f = frequency of the median class = 14
h = width of the class interval (assuming all classes are of the same width) = 2
• Substituting the values, we get:
• Numerator = (ⁿ⁄₂ - cf) = (³⁵⁄₂ - 14)  = (17.5-14) = 3.5
• Thus median = 46 + (^3.5⁄₁₄)×2 = 46 + 0.5 = 46.5 (Same as before)

Solved example 37.17
The following table gives production yield per hectare of wheat of 100 farms of a village.

Table.37.59

Change the distribution to a more than type distribution, and draw its ogive.
Solution:
1. To draw the more than ogive:
• We want the the lower limit of each class interval to use as the x coordinates
• We want the corresponding values in the 'more than' cumulative frequency column to be used as the y coordinates
• So x coordinates are already available in the question.

The y coordinates can be obtained from the cumulative frequency tabulated in the third column of the table 37.60 below:

Table.37.60

2. So the coordinates are:
(50,100), (55, 98), (60,90), (65,78), (70,54), (75,16)
• The required ogive is shown in fig.37.10 below:

Fig.37.10

---

We have completed this discussion on topics in statistics. Next, we will be discussing class 11 math topics.

PREVIOUS      CONTENTS       NEXT



                        Copyright©2018 High school Maths lessons. blogspot.in - All Rights Reserved

Chapter 37.6 - The Ogive curve

In the previous section we completed a discussion about median. In this section we will see Ogive curves.
• We know that one picture can replace a thousand words. We have seen examples of this in our previous discussions in statistics (part II). There we saw bar graphs, histograms, frequency polygons etc., 
• We saw that those graphs help to get an understanding about the data at a glance. 
• In our present discussion, we have not yet drawn any graphs. So let us try to 'represent pictorially', what we have learned so far in this chapter. We will write it in steps:

1. Consider the table 37.39 that we saw earlier. It is shown again below:

Table.37.39

• Let us plot the cumulative frequencies along the y axis
• Then the class intervals will be plotted along the x axis
• But we see that each class interval has two values: a lower limit and an upper limit. Which one will we use for plotting?
2. Let us choose the upper limits
• Then the coordinates of the points on the graphs will be: 
(10,5), (20,8), (30,12), (40,15), . . . , (100,53)
• The graph thus obtained is shown in fig.37.1 below:

Fig.37.1

• Note that the scale need not be the same for both the axes
• The curve (shown in magenta colour) joining the points is called a cumulative frequency curve or an ogive
3. So we know how to draw an ogive. Let us now see it's features:
• Suppose we want to know the cumulative frequency corresponding to a class 70-80
• Then we take the point on the graph at which the x coordinate is 80
• At that point, the y coordinate is 38. 
• That means the cumulative frequency at that point is 38
• So the cumulative frequency corresponding to class 70-80 is 38
• That means, 38 observations in the given data have a value lesser than 80
4. In our present example, the observations are: 'marks obtained by 53 students'
• So we can write:
38 students have marks less than 80
• If the observations are 'weights', we can write:
38 students have weights less than 80 kg
• If the observations are 'lengths of leaves', we can write:
38 leaves have length less than 80 mm'
5. So it is a convenient way to get a quick understanding about the data
• Note that we use less than 80. This is because, if there is a mark equal to 80, it will not be included in the class 70-80. It will be included only in 80-90
• So all marks equal to and greater than 80 will be on the right side of (80,38)
6. So which ever point we consider in the graph in fig.37.1 above, we get valuable information. We will break down the information as follows:
(i) The coordinates of the point will be in the form: (x coordinate, y coordinate)
(ii) 'y coordinate' number of students have scored less than 'x coordinate' marks
An example:
• Take class mark 50 on the x axis
• The y coordinate corresponding to it is 18. So we have: (50,18)
■ We can write:
18 students have scored less than 50 marks
7. So the graph in fig.37.1 is marked as 'Less than ogive'
8. (80, 38) and (50,18) are points already written on the ogive. We can get information on other points also:
(i) Consider the score 75. We want to know how many students got less than 75
(ii) For that, mark a point R at (75,0) on the x axis. 
(iii) Draw a vertical dashed line (shown in white colour in fig.37.2 below) through R

Fig.37.2

(iv) Let it intersect the ogive at Q
(v) Draw a horizontal white dashed line through Q
(vi) Let it intersect the y axis at P
(vii) Note down the 'y coordinate' of P. It is 33.5
• We can write:
About 33 students have scored less than 75 marks
• Note that, if we are using a graph paper, we will not need to draw the dashed lines. They will be already present in the form of thin lines. 

---

So we have seen the Less than ogive. Is there a 'More than ogive' ? Let us see:
1. Consider the table 37.40 that we saw earlier. It is from the same problem. It is shown again below:

Table.37.40

• Let us plot the cumulative frequencies along the y axis
• Then the class intervals will be plotted along the x axis
• But we see that each class interval has two values: a lower limit and an upper limit. Which one will we use for plotting?
2. Let us choose the lower limits
• Then the coordinates of the points on the graphs will be: 
(0,53), (10,48), (20,45), (30,41), . . . , (90,8)
• The graph thus obtained is shown in fig.37.3 below:

Fig.37.3

• Note that the scale need not be the same for both the axes
• The curve (shown in yellow colour) joining the points is a cumulative frequency curve or an ogive
3. So we know how to draw this new type of ogive also. Let us now see it's features:
• Suppose we want to know the cumulative frequency corresponding to a class 70-80
• Then we take the point on the graph at which the x coordinate is 70
• At that point, the y coordinate is 24. 
• That means the cumulative frequency at that point is 24
• So the cumulative frequency corresponding to class 70-80 is 24
• That means, 24 observations in the given data have a value more than 70
4. In our present example, the observations are: marks obtained by 53 students
• So we can write:
24 students have marks more than 70
• If the observations are 'weights', we can write:
24 students have weights more than 70 kg
• If the observations are 'lengths of leaves', we can write:
24 leaves have length more than 70 mm
5. So it is a convenient way to get a quick understanding about the data
• Note that we use more than 70. 
6. So which ever point we consider in the graph in fig.37.2 above, we get valuable information. We will break down the information as follows:
(i) The coordinates of the point will be in the form: (x coordinate, y coordinate)
(ii) 'y coordinate' number of students have scored more than 'x coordinate' marks
An example:
• Take class mark 50 on the x axis
• The y coordinate corresponding to it is 35. So we have: (50,35)
■ We can write:
35 students have scored more than 50 marks
7. So the graph in fig.37.3 is marked as 'More than ogive'
8. (70, 24) and (50,35) are points already written on the ogive. We can get information on other points also. 
• For that, draw the required vertical and horizontal dashed lines just as we saw in the case of less than ogive.

---

Now we will see an interesting application of the 'less than ogive'. We will write it in steps:
1. In fig.37.2 above, we started to work from point R which is on the x axis. 
• Then we reached Q and then finally P, which is on the y axis. 
• The point P gave us the 'number of students'
2. How about working in a reverse order?
• If we start from a point P on the y axis, we will be starting with a 'particular number of students'
• When we reach the x axis, we will get a 'particular score' Q
• The no. of students at P will have scored less than the marks at Q
3. Do we have any 'particular number of students' which might be of interest?
• We certainly do. 
• 'Half the number' is often an important point in any data. It is related to 'the median'
• In our present case, the median is (⁵³⁄₂) = 26.5
4. So we mark P (0,26.5) on the y axis and start from there. The path to R on the x axis is shown in fig.37.4 below:

Fig.37.4

• We get R (66.4,0). So we can write:
About 26 students scored less than 66.4 The other 26 scored more than 66.4
• In other words, 66.4 is the median score
■ So it is clear: To find the median, mark (0,ⁿ⁄₂) on the y axis and work towards the x axis
5. We proved it using a less than ogive. Will it work on a more than ogive?
The path from P to R is marked on the more than ogive in fig.37.5 below:

Fig.37.5

• We get the same result: The median is 66.4
7. So it means that point Q has the same coordinates in both less than and more than ogives
That is., Q is common in both the curves
In other words, Q is the point of intersection of the two curves. This is shown in the fig.37.6 below:

Fig.37.6

8. So, instead finding (ⁿ⁄₂) and then drawing horizontal and vertical dashed lines, we can do the following steps:
(i) Draw both the ogives 
(ii) Mark the point of intersection Q
(iii) Draw a vertical dashed line through Q. Let it meet the x axis at R
(iv) then the x coordinate of R is the median

---

An example:
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution :

Table.37.53

Draw both ogives for the data above. Hence obtain the median profit.
Solution:
1. We are given a cumulative frequency table. 
• The cumulative frequencies in the second column can be used to draw the more than ogive. But those cumulative frequencies will give only the y coordinates of the points. 
• To know the x coordinates, we need class intervals. 
2. So we will convert the given 'cumulative frequency distribution table' into a 'grouped frequency distribution table':
• Consider the first row of the given table:
All the shops are making a profit of more than or equal to 5 lakhs 
• Consider the second row of the given table:
28 shops are making a profit of more than or equal to 10 lakhs 
• 'More than or equal to 10' will include 'more than or equal to 5' also
• So number of shops making a profit of more than 5 lakhs but less than 10 lakhs is (30-28) = 2
• So the frequency corresponding to class 5-10 will be 2
• This is shown in the first row of our new table 37.54 below
3. Consider the third row of the given table:
• 16 shops are making a profit of more than or equal to 15 lakhs 
• 'More than or equal to 15' will include 'more than or equal to 10' also
• So number of shops making a profit of more than 10 lakhs but less than 15 lakhs is (28-16) = 12
• So the frequency corresponding to class 10-15 will be 12
• This is shown in the second row of our new table 37.54 below
4. Consider the fourth row of the given table:
• 14 shops are making a profit of more than or equal to 20 lakhs 
• 'More than or equal to 20' will include 'more than or equal to 15' also
• So number of shops making a profit of more than 15 lakhs but less than 20 lakhs is (16-14) = 2
• So the frequency corresponding to class 15-20 will be 2
• This is shown in the third row of our new table 37.54 below

Table.37.54

In this way we can continue up to the last row. But once we understand the pattern, the columns can be easily filled up.
5. Now we can draw the ogives. 
(i) First we will draw the less than ogive.
• We know that, for the less than ogive, the x coordinates are the upper limits of the class intervals
• y coordinates are the cumulative frequencies of the less than type. This is given in the third column of the above table 37.53
    ♦ As usual, this column is easily filled up using the pattern
• So the coordinates will be: (10,2), (15,14), (20,16), . . . , (40,30)
• The curve joining these points is the less than ogive of this problem. It is shown in magenta colour in fig.37.7 below:

Fig.37.7

• A sample:
    ♦ (30,23) is a point on the less than ogive
    ♦ So there are 23 shops which make a profit of less than 23 lakhs
(ii) Now we will draw the more than ogive.
• We know that, for the more than ogive, the x coordinates are the lower limits of the class intervals
• y coordinates are the cumulative frequencies of the more than type. They were given to us in the question. They are shown again in the fourth column of the above table 37.53
• So the coordinates will be: (5,30), (10,28), (15,16), . . . , (35,3)
• The curve joining these points is the more than ogive of this problem. It is shown in yellow colour in fig.37.7 above.
• A sample:
    ♦ (25,10) is a point on the more than ogive
    ♦ So there are 10 shops which make a profit of more than 25 lakhs
6. To find the median:
• Let the two ogives intersect at Q. From Q, draw a vertical dashed line. It will intersect the x axis at R
• The coordinates of R are (17.5,0)
• So the median profit is 17.5 lakhs
• Note that, the y coordinate of Q is 15.
    ♦ This 15 is equal to (ⁿ⁄₂) = (³⁰⁄₂)
7. Conclusion:
• If we arrange all the 30 shops in the increasing order of profit, the shop which makes a profit of 17.5 lakhs will come in the middle.
• There will be about 15 shops on the left of this shop. Each of their profits will be less than 17.5 lakhs
• There will be about 15 shops on the right of this shop. Each of their profits will be more than 17.5 lakhs

---

The term ‘ogive’ is pronounced as ‘ojeev’ and is derived from the word 'ogee'. An ogee is a curved shape consisting of  concave and convex arcs. It was used to form arches of buildings in the 14th and 15th century Gothic styles. Our ogive curves in statistics resemble those curves, and so the name was given.

---

In the next section, we will see some solved examples.

The link below gives the notes on statistics of class 11:

Mean deviation and Standard deviation.

PREVIOUS      CONTENTS       NEXT

 
                        Copyright©2018 High school Maths lessons. blogspot.in - All Rights Reserved

Chapter 37.5 - Calculation of Median - Solved examples

In the previous section we discussed about median. We also saw some examples. In this section we will see a few more examples.

Example 11
The median of the following data is 525. Find the values of x and y, if the total frequency is 100.

Table.37.43

Solution:
1. In the given data, two frequencies are missing. They are given as 'x' and 'y'
• However, we will proceed as usual, as if to find the median
• The first step to find the median, is to fill up the cumulative frequency column. It is shown in table 37.44 below:

Table.37.44

2. The median is given to us as 525. It falls within the class 500-600
• So 500-600 is the median class
3. Now we can apply the formula:
■ The median is calculated using the following formula:

Where:
Median = 525 (Already given in this problem)
l = lower limit of the median class = 500
n = number of observations = total of the frequency column = (76+x+y) = 100 (given)
cf = cumulative frequency of the class preceding the median class = (36+x)
f = frequency of the median class = 20
h = width of the class interval (assuming all classes are of the same width) = 100
• Substituting the values, we get:
Numerator = (ⁿ⁄₂ - cf) = [¹⁰⁰⁄₂ - (36+x)]  = [50-36-x] = [14-x]
• Thus median = 525 = 500 + [^(14-x)⁄₂₀]×100 
⟹ 525 = 500 + 5(14-x)
⟹ 25 = 5(14-x) ⟹ 14-x = 5 ⟹ x = 9
4. We are given that total frequency = 100
• So we can write: 76+x+y = 100 ⟹ x+y = 24
• Substituting x = 9, we get:
y = 24 - 9 = 15

---

Now we will see some solved examples
Solved example 37.11
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.

Table.37.45

Solution:
• We will form the complete table from which we can find all the three values: mean, median and mode. 
• It is the same type of table that we saw in the case of mean. The only change is the extra column for 'cumulative frequency'. It is shown in magenta colour:

Table.37.46

1. First we will find the mean
We will use the step deviation method:
• u is given by the formula:

• The numerator is the value at the bottom end of the eighth column. It is 43
• The denominator is the value at the bottom end of the second column. It is 80
• So we get u = ⁷⁄₆₈ 
• Thus x = a + hu = [135 + (20 × ⁷⁄₆₈)] = 137.06
2. Now we will find the mode
(i) The modal class is the class interval having the highest frequency
• So in this problem, the class interval '125- 145' is the modal class. It has the highest frequency of '20' 
(ii) Now we can calculate the mode using the formula:

l = lower limit of the modal class = 125
h = width of the class interval (assuming all classes are of the same width) = 20
f₁ = frequency of the modal class = 20
f₀ = frequency of the class preceding the modal class = 13
f₂ = frequency of the class succeeding the modal class = 14
Substituting all the values, we get:
mode = 125 + (^20-13⁄_2×20-13-14)×20 = 125 + (⁷⁄_40-27)×20 = 135.77
3. Now we will calculate the median:
• In this problem, the total number of observations 'n' = 68. This is an even number.
So ⁿ⁄₂ = ⁶⁸⁄₂ = 34
• The cumulative frequency closest to and just greater than 34 is 42
• The class corresponding to the cumulative frequency 42 is 125-145
• So 125-145 is the median class. It's frequency = 20
■ The median is calculated using the following formula:

Where:
l = lower limit of the median class = 125
n = number of observations = 68
cf = cumulative frequency of the class preceding the median class = 22
f = frequency of the median class = 20
h = width of the class interval (assuming all classes are of the same width) = 20
• Substituting the values, we get:
• Numerator = (ⁿ⁄₂ - cf) = (⁶⁸⁄₂ - 22)  = (34-22) = 12
• Thus median = 125 + (¹²⁄₂₀)×20 = 125 + 12 = 137
■ We can write the conclusion:
1. Mean is obtained as 137.06 units:
(i) The average consumption of electricity in that locality in a month = 137.06
(ii) There are 68 families. So the total consumption will be about (137.06 × 68) = 9320.08 units
(iii) Even if there are more than 68 families, this mean can be used.
(iv) For example, if there are 450 families, the total consumption in a month in that locality will be (137.06 × 450) = 61677 units
2. Mode is obtained as 135.77:
(i) Among the 68 families, 'number of families consuming 135.77 units per month' is more than others
(ii) If we list the monthly consumption of each of the 68 families individually, the 'value 135.77 units' will occur more no. of times than others 
3. Median is obtained as 137 units
(i) If we list the monthly consumption of all the 68 families in the ascending order, 137 will occupy nearly the 34^th position.
(ii) The values to the left of 137 will be less and the values to the right will be more

Solved example 37.12
If the median of the distribution given below is 28.5, find the values of x and y

Table.37.47

Solution:
1. In the given data, two frequencies are missing. They are given as 'x' and 'y'
• However, we will proceed as usual, as if to find the median
• The first step to find the median, is to fill up the cumulative frequency column. It is shown in table 37.48 below:

Table.37.48

2. The median is given to us as 28.5. It falls within the class 20-30
• So 20-30 is the median class
3. Now we can apply the formula:
■ The median is calculated using the following formula:

Where:
Median = 28.5 (Already given in this problem)
l = lower limit of the median class = 20
n = number of observations = total of the frequency column = (45+x+y) = 60 (given)
cf = cumulative frequency of the class preceding the median class = (5+x)
f = frequency of the median class = 20
h = width of the class interval (assuming all classes are of the same width) = 10
• Substituting the values, we get:
Numerator = (ⁿ⁄₂ - cf) = [⁶⁰⁄₂ - (5+x)]  = [30-5-x] = [25-x]
• Thus median = 28.5 = 20 + [^(25-x)⁄₂₀]×10 
⟹ 28.5 = 20 + ¹⁄₂ × (25-x)
⟹ 8.5 = ¹⁄₂ × (25-x) ⟹ 17 = (25-x) ⟹ x = 8
4. We are given that total frequency = 60
• So we can write: 45+x+y = 60 ⟹ x+y = 15
• Substituting x = 8, we get:
y = 15 - 8 = 7

Solved example 37.13
A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years on wards but less than 60 year

Table.37.49

Solution:
1. The given data is in the form of a cumulative frequency table. 
We have to convert it into a 'grouped frequency distribution table'. Let us write the steps:
• No. of policy holders below age 20 is 2
• No. of policy holders below age 25 is 6
• This 6 will include the 'no. of policy holders of ages below 20' also
2. From the above three information, we can find the 'no. of policy holders whose ages satisfy the following two conditions':
    ♦ No. of ages greater than or equal to 20
    ♦ No. of ages less than 25
• Obviously, the no. of ages satisfying the two conditions is: (6-2) = 4
• So 4 policy holders satisfy the condition: 20 ≤ age < 25
• Those 4 policy holders will obviously fall in the class: 20-25
• In other words, the frequency of the class 20-25 is 4
3. So we separated out 4 policy holders from 6
What about the remaining 2?
• They satisfy the condition: 'age < 20'
• Those 2 policy holders will obviously fall in the class: k-20
    ♦ Where 'k' is any number less than 20. We will give it a value 15
• So the frequency of the class 15-20 is 2
4. So we found two classes: 
    ♦ class 15-20 with frequency 2
    ♦ class 20-25 with frequency 4
Now we consider the next cumulative frequency, which is 24:
• No. of policy holders below age 25 is 6
• No. of policy holders below age 30 is 24
• This 24 will include the 'no. of policy holders of ages below 25' also
• From the above three information, we can find the 'no. of policy holders whose ages satisfy the following two conditions':
    ♦ No. of ages greater than or equal to 25
    ♦ No. of ages less than 30
• Obviously, the no. of ages satisfying the two conditions is: (24-6) = 18
• So 18 policy holders satisfy the condition: 25 ≤ age < 30
• Those 18 policy holders will obviously fall in the class: 25-30
• In other words, the frequency of the class 25-30 is 18
5. Thus so far, we found three classes: 
    ♦ class 15-20 with frequency 2
    ♦ class 20-25 with frequency 4
    ♦ class 25-30 with frequency 18
Now we consider the next cumulative frequency, which is 45:
• No. of policy holders below age 30 is 24
• No. of policy holders below age 35 is 45
• This 45 will include the 'no. of policy holders of ages below 30' also
• From the above three information, we can find the 'no. of policy holders whose ages satisfy the following two conditions':
    ♦ No. of ages greater than or equal to 30
    ♦ No. of ages less than 35
• Obviously, the no. of ages satisfying the two conditions is: (45-24) = 21
• So 21 policy holders satisfy the condition: 30 ≤ age < 35
• Those 21 policy holders will obviously fall in the class: 30-35
• In other words, the frequency of the class 30-35 is 21
• Thus so far, we found four classes:
    ♦ class 15-20 with frequency 2
    ♦ class 20-25 with frequency 4
    ♦ class 25-30 with frequency 18 
    ♦ class 30-35 with frequency 21
■ We can go on like this until we reach the end of the table. However, once we understand the pattern, the frequencies of each class can be easily calculated. The resulting table is shown below:

Table.37.50

• Note how easy it is to fill up the 'frequency column':
To fill up any one row in the 'frequency column', do these steps:
(i) Take the value coming in the same row in the 'cumulative frequency column'
(ii) Take the value coming in the row just above in the 'cumulative frequency column'
(iii) Subtract (ii) from (i)
6. Now we can begin the calculations for the median:
• In this problem, the total number of observations 'n' = 100. This is an even number.
So ⁿ⁄₂ = ¹⁰⁰⁄₂ = 50
• The cumulative frequency closest to 50 and greater than 50 is 78
• The class corresponding to the cumulative frequency 78 is 35-40
• So 35-40 is the median class. It's frequency = 33
■ The median is calculated using the following formula:

Where:
l = lower limit of the median class = 35
n = number of observations = 100
cf = cumulative frequency of the class preceding the median class = 45
f = frequency of the median class = 33
h = width of the class interval (assuming all classes are of the same width) = 5
• Substituting the values, we get:
• Numerator = (ⁿ⁄₂ - cf) = (¹⁰⁰⁄₂ - 45)  = (50-45) = 5
• Thus median = 35 + (⁵⁄₃₃)×5 = 35 + 0.76 = 35.76
7. We can write the conclusion:
(i) If we list the ages of all the 100 policy holders in the ascending order, 35.76 will occupy nearly the 50^th position.
(ii) The ages to the left of 35.67 will be less and the ages to the right will be more

Solved example 37.14
The lengths of 40 leaves of a plant are measured correct to the nearest mm, and the data obtained is represented in the following table:

Table.37.51

Find the median length of the leaves
Solution:
1. The class intervals in the given table are not continuous. We can apply the formula for median only if the class intervals are continuous.
We know how to make them continuous (Details here).
So the new class intervals are given in table 37.52 below. The cumulative frequencies are also shown along with it.

Table.37.52

2. Now we can begin the calculations for the median:
• In this problem, the total number of observations 'n' = 40. This is an even number.
So ⁿ⁄₂ = ⁴⁰⁄₂ = 20
• The cumulative frequency closest to 20 and greater than 20 is 29
• The class corresponding to the cumulative frequency 29 is 144.5-153.5
• So 144.5-153.5 is the median class. It's frequency = 12
■ The median is calculated using the following formula:

Where:
l = lower limit of the median class = 144.5
n = number of observations = 40
cf = cumulative frequency of the class preceding the median class = 17
f = frequency of the median class = 12
h = width of the class interval (assuming all classes are of the same width) = 9
• Substituting the values, we get:
• Numerator = (ⁿ⁄₂ - cf) = (⁴⁰⁄₂ - 17)  = (20-17) = 3
• Thus median = 144.5 + (³⁄₁₂)×9 = 144.5 + 2.25 = 146.75
3. We can write the conclusion:
(i) If we arrange all the 40 leaves in the ascending order of their lengths, the leaf with 146.75 mm length will occupy nearly the 20^th position.

---

■ We have discussed about the three measures of central tendency: Mean, mode and median. Each of them have their merits and demerits. So they are used according to the 'end result to be achieved'. 
• Let us see an example:
• Mean of five lengths 32, 35, 30, 39 and 38 is: (¹⁷⁴⁄₅) = 34.8 cm
• If a sixth length 34 cm is also added, the mean of 6 heights is: (²⁰⁸⁄₆) = 34.67
• If the sixth height added is 2 instead of 34, the mean will be (¹⁷⁶⁄₆) = 29.33
• When the sixth length added is 34, the mean changed from 34.8 to 34.67. This is only a mild change
• When the sixth length added is 2 instead of 34, the mean changed from 34.8 to 29.33. This is a significant change 
• So we see that extreme values in a group will in influence the mean. 
• In other words, if extreme values are present, the mean will not give the true nature of the data
• At the same time, it may not be permissible to discard the extreme values.
• So the decision about 'using mean or median' depends on the situation
• If individual values need not be presented in the result, we can use median. It gives an accurate value at the middle. Again it depends on the situation
■ Mode is used when we want the most repeating value. Examples are:
Mostly watched TV shows, Mostly preferred shoes, Mostly preferred colour for car etc.,

---

■ There is a empirical relationship between the three measures of central tendency :

3 Median = Mode + 2 Mean
Let us check:
1. Consider the solved example 37.11 above. In that example, we obtained all the results:
• mean = 137.06
• mode = 135.77
• median = 137
2. Left side = 3 times median = 3 × 137 = 411
3. Right side = (mode + 2 times mean) = (135.77 + 2 × 137.06) = (135.77 + 274.12) = 409.89
• The two sides are approximately equal

---

In the next section, we will see ogive curves.

PREVIOUS      CONTENTS       NEXT

 
                        Copyright©2018 High school Maths lessons. blogspot.in - All Rights Reserved