In the previous section we discussed about the Pythagoras theorem. In this section we continue the discussion. Later in this section we will see some solved examples.
Let us do another experiment: Make cardboard cut outs of three squares of different sizes. One with side 8 cm, the second with side 9 cm, and the third with side 10 cm. Arrange them in such a way that one side of each square becomes a side of a triangle. This is shown in the fig.9.25 below:
So we have a triangle with sides 8, 9 and 10 cm. Measure each of the three angles of this triangle. We find that none of them are 90. So no corner of this triangle has 90 and thus, it is not a right angled triangle.
The hypotenuse is the side opposite to 90 corner. So this triangle does not have a hypotenuse. Even then, let us try to apply Pythagoras theorem: 92 + 82 must be equal to 102
But 92 + 82 = 81 + 64 = 145 And, 102 = 100. So they are not equal. That is.,
92 + 82 ≠ 102. We find this 'not equal to condition' in the other two combinations also of this triangle:
102 + 82 ≠ 92 and, 92 + 102 ≠ 82. So we can say that: if the square of the hypotenuse is equal to the sum of the squares of the legs, then it is a right angled triangle. This is the converse of the Pythagoras theorem. So we can write:
Pythagoras theorem:
In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.
Converse of Pythagoras theorem:
If the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then it is a right angled triangle. The longest side is the hypotenuse, and the other two sides are the legs.
We will now see some solved examples:
Solved example 9.15
Find the value of x in the following figs.
Solution:
(a) • x is the side opposite to the 90o angle. So x is the hypotenuse, and the other two are the legs
• Applying the Pythagoras theorem, we get x2 = 32 + 42 ⇒ x2 = 9 + 16 = 25
∴ x = √25 = 5
(b) • x is the side opposite to the 90o angle. So x is the hypotenuse, and the other two are the legs
• Applying the Pythagoras theorem, we get x2 = 62 + 82 ⇒ x2 = 36 + 64 = 100
∴ x = √100 = 10
(c) We can consider the given triangle as two smaller triangles. One on the left and the other on the right. We need to do the calculations on one triangle only because, the other triangle is symmetrical.
• So 37 is the hypotenuse. 12 and x/2 are the legs
• Applying the Pythagoras theorem, we get 372 = 122 + (x/2)2 ⇒ (x/2)2 = 372 - 122 = 1369 - 144 = 1225 ⇒ x/2 = √1225 = 35
∴ x = 35 × 2 = 70
Solved example 9.16
A ladder is leaning against a wall as shown in the fig.9.27(a) below. The height of the wall above the top end of the ladder is 1.2 m. The foot of the ladder is 1.5 m away from the wall. If the length of the ladder is 2.5 m, find the total height of the wall
Solution: Fig.9.27(b) shows the side view. From the side view, it is clear that, the leaning ladder forms a right angled triangle (shown in yellow colour) with the wall.
• The length 2.5 m of the ladder forms hypotenuse.
• The distance 1.5 m of the foot of the ladder from the wall forms one leg.
• Let us put the unknown length of the other leg as 'x'
• Applying the Pythagoras theorem, we get 2.52 = 1.52 + x2 ⇒ x2 = 2.52 - 1.52 = 6.25 - 2.25 = 4
∴ x = √4 = 2.0 m
• So the total height of the wall = 2 + 1.2 = 3.2 m
Solved example 9.17
A post is broken at a height of 5 m from the ground. The top end of the post now touches the ground at a distance of 12 m from the base of the post. Calculate the original height of the post.
Solution:
Fig.9.28(a) shows the rough sketch. We have to first calculate the length BC
• Applying the Pythagoras theorem, we get BC2 = AB2 + AC2 ⇒ BC2 = 122 + 52 = 144 + 25 = 169
∴ BC = √169 = 13
• So the original height of the post = 5 + 13 = 18 m
Solved example 9.18
After carefully studying the triangle in fig.9.28(b), pick out the true statement from those given below:
(i) XY2 = XZ2 + YZ2 (ii) XZ2 = XY2 + YZ2 (iii) YZ2 = XY2 + XZ2
Solution:
• ∠ZXY = 35o and ∠XZY = 55o
• The sum of these two angles = 35 + 55 = 90o
• So the third ∠XYZ = 180 - 90 = 90o (∵ sum of interior angles of a triangle is 180o)
• So this is a right angled triangle, with the 90o angle at Y
• Thus XZ, which is the side opposite to corner Y, is the hypotenuse
• So the true statement is (ii): XZ2 = XY2 + YZ2
Solved example 9.19
Length of a rectangle is 40 cm. It's diagonal has a length of 41 cm. What is the perimeter?
Solution:
A rough sketch is shown in the fig.9.28(c). ABCD is the rectangle whose length is 40 cm. It's width is not given. We need to find the width BC or AD to calculate the perimeter.
• When the diagonal AC is drawn, the rectangle is split into two right angled triangles ABC and ACD.
• Consider the triangle ABC. AC is the hypotenuse, AB and BC are the legs
• Applying the Pythagoras theorem, we get AC2 = AB2 + BC2 ⇒ BC2 = AC2 - AB2 = 412 - 402 = 1681 - 1600 = 81
∴ BC = √81 = 9 cm
• So the perimeter = 2(AB + BC) = 2(40 + 9) = 2 × 49 = 98 cm
In the next chapter we will discuss about Congruence of Triangles.
Let us do another experiment: Make cardboard cut outs of three squares of different sizes. One with side 8 cm, the second with side 9 cm, and the third with side 10 cm. Arrange them in such a way that one side of each square becomes a side of a triangle. This is shown in the fig.9.25 below:
 |
| Fig.9.25 |
The hypotenuse is the side opposite to 90 corner. So this triangle does not have a hypotenuse. Even then, let us try to apply Pythagoras theorem: 92 + 82 must be equal to 102
But 92 + 82 = 81 + 64 = 145 And, 102 = 100. So they are not equal. That is.,
92 + 82 ≠ 102. We find this 'not equal to condition' in the other two combinations also of this triangle:
102 + 82 ≠ 92 and, 92 + 102 ≠ 82. So we can say that: if the square of the hypotenuse is equal to the sum of the squares of the legs, then it is a right angled triangle. This is the converse of the Pythagoras theorem. So we can write:
Pythagoras theorem:
In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.
Converse of Pythagoras theorem:
If the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then it is a right angled triangle. The longest side is the hypotenuse, and the other two sides are the legs.
We will now see some solved examples:
Solved example 9.15
Find the value of x in the following figs.
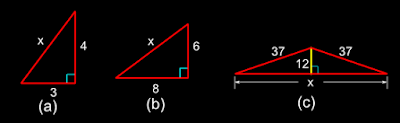 |
| Fig.9.26 |
(a) • x is the side opposite to the 90o angle. So x is the hypotenuse, and the other two are the legs
• Applying the Pythagoras theorem, we get x2 = 32 + 42 ⇒ x2 = 9 + 16 = 25
∴ x = √25 = 5
(b) • x is the side opposite to the 90o angle. So x is the hypotenuse, and the other two are the legs
• Applying the Pythagoras theorem, we get x2 = 62 + 82 ⇒ x2 = 36 + 64 = 100
∴ x = √100 = 10
(c) We can consider the given triangle as two smaller triangles. One on the left and the other on the right. We need to do the calculations on one triangle only because, the other triangle is symmetrical.
• So 37 is the hypotenuse. 12 and x/2 are the legs
• Applying the Pythagoras theorem, we get 372 = 122 + (x/2)2 ⇒ (x/2)2 = 372 - 122 = 1369 - 144 = 1225 ⇒ x/2 = √1225 = 35
∴ x = 35 × 2 = 70
Solved example 9.16
A ladder is leaning against a wall as shown in the fig.9.27(a) below. The height of the wall above the top end of the ladder is 1.2 m. The foot of the ladder is 1.5 m away from the wall. If the length of the ladder is 2.5 m, find the total height of the wall
 |
| Fig.9.27 |
• The length 2.5 m of the ladder forms hypotenuse.
• The distance 1.5 m of the foot of the ladder from the wall forms one leg.
• Let us put the unknown length of the other leg as 'x'
• Applying the Pythagoras theorem, we get 2.52 = 1.52 + x2 ⇒ x2 = 2.52 - 1.52 = 6.25 - 2.25 = 4
∴ x = √4 = 2.0 m
• So the total height of the wall = 2 + 1.2 = 3.2 m
Solved example 9.17
A post is broken at a height of 5 m from the ground. The top end of the post now touches the ground at a distance of 12 m from the base of the post. Calculate the original height of the post.
Solution:
Fig.9.28(a) shows the rough sketch. We have to first calculate the length BC
• Applying the Pythagoras theorem, we get BC2 = AB2 + AC2 ⇒ BC2 = 122 + 52 = 144 + 25 = 169
∴ BC = √169 = 13
• So the original height of the post = 5 + 13 = 18 m
Solved example 9.18
After carefully studying the triangle in fig.9.28(b), pick out the true statement from those given below:
(i) XY2 = XZ2 + YZ2 (ii) XZ2 = XY2 + YZ2 (iii) YZ2 = XY2 + XZ2
Solution:
• ∠ZXY = 35o and ∠XZY = 55o
• The sum of these two angles = 35 + 55 = 90o
• So the third ∠XYZ = 180 - 90 = 90o (∵ sum of interior angles of a triangle is 180o)
• So this is a right angled triangle, with the 90o angle at Y
• Thus XZ, which is the side opposite to corner Y, is the hypotenuse
• So the true statement is (ii): XZ2 = XY2 + YZ2
Solved example 9.19
Length of a rectangle is 40 cm. It's diagonal has a length of 41 cm. What is the perimeter?
Solution:
A rough sketch is shown in the fig.9.28(c). ABCD is the rectangle whose length is 40 cm. It's width is not given. We need to find the width BC or AD to calculate the perimeter.
• When the diagonal AC is drawn, the rectangle is split into two right angled triangles ABC and ACD.
• Consider the triangle ABC. AC is the hypotenuse, AB and BC are the legs
• Applying the Pythagoras theorem, we get AC2 = AB2 + BC2 ⇒ BC2 = AC2 - AB2 = 412 - 402 = 1681 - 1600 = 81
∴ BC = √81 = 9 cm
• So the perimeter = 2(AB + BC) = 2(40 + 9) = 2 × 49 = 98 cm
In the next chapter we will discuss about Congruence of Triangles.
No comments:
Post a Comment