In the previous section we saw the method to determine whether a given set of 3 lengths form a triangle or not. We also saw some solved examples. In this section, we will see more solved examples.
Solved example 9.8
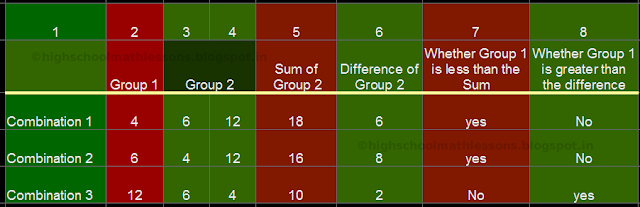
Check whether three lengths of 38, 22 and 14 cm can be used to form a triangle
Solution:
We do not have 6 'yes'. So this triangle is not possible.
Solved example 9.9
Check whether the three lengths of 34, 22 and 14 cm can be used to form a triangle
Solution:
We have a total of 6 'yes'. So it is possible to form this triangle.
Solved example 9.10
Check whether the three lengths of 4, 6 and 12 cm can be used to form a triangle
Solution:
We do not have 6 'yes'. So this triangle is not possible.
Solved example 9.11
Lengths of two sides of a triangle are 22 cm and 14 cm. Then between which two numbers should the third side fall?
Solution:
• The lengths of two sides are given as 22 and 14 cm
• We know that in any triangle, any one side should be less than the sum of the other two sides. So here, the third side should be less than 22 + 14 = 36 cm.
• We know that in any triangle, any one side should be greater than the difference between the other two sides. So here, the third side side should be greater than 22 - 14 = 8 cm.
• Thus we can say, the length of the third side should fall between 8 cm and 36 cm
Solved example 9.12
Lengths of two sides of a triangle are 6 cm and 12 cm. Then between which two numbers should the third side fall?
Solution:
• The lengths of two sides are given as 6 and 12 cm
• We know that in any triangle, any one side should be less than the sum of the other two sides. So here, the third side should be less than 6 + 12 = 18 cm.
• We know that in any triangle, any one side should be greater than the difference between the other two sides. So here, the third side side should be greater than 12 - 6 = 6 cm.
• Thus we can say, the length of the third side should fall between 18 cm and 6 cm
A graphical representation of the answers of the above two problems are shown below:
The lengths of the blue lines are not allowed for the third side. The top of the third side should fall between the horizontal green lines. The top of one blue line is below a green line. The top of the other blue line is above a green line. So they do not help to complete the triangle.
Solved example 9.13
In the triangle ABC shown in fig.9.20(a) below, prove that BC < OB + OC
Solution:
• In the given triangle ABC, we can think of a smaller triangle BCO inside ABC.
• In this smaller triangle, if we take out BC, the other two sides are OB and OC.
• So one side is BC, and the other two sides are OB and OC.
• We know that any one side should be less than the sum of the other two sides.
• So we can write: BC < OB + OC
• In a similar way, we can prove:
AC < OA + OC and AB < OA + OB
Solved example 9.14
In the Δ PQR, a median RM is drawn fig.9.20(b). Prove that the sum of the three sides of the Δ PQR is greater than the median RM
Solution:
We have to prove that PQ + PR + QR > 2 RM:
• In Δ PRM, PM + PR > RM
• In Δ QRM, QR + QM > RM
• Adding the above two, we get: PM + PR + QR + QM > RM + RM
⇒ PQ + PR + QR > 2 RM (∵ PM + QM = PQ)
In the next section we will learn about Pythagoras Theorem.
Solved example 9.8
Check whether three lengths of 38, 22 and 14 cm can be used to form a triangle
Solution:
We do not have 6 'yes'. So this triangle is not possible.
Solved example 9.9
Check whether the three lengths of 34, 22 and 14 cm can be used to form a triangle
Solution:
We have a total of 6 'yes'. So it is possible to form this triangle.
Solved example 9.10
Check whether the three lengths of 4, 6 and 12 cm can be used to form a triangle
Solution:
We do not have 6 'yes'. So this triangle is not possible.
Solved example 9.11
Lengths of two sides of a triangle are 22 cm and 14 cm. Then between which two numbers should the third side fall?
Solution:
• The lengths of two sides are given as 22 and 14 cm
• We know that in any triangle, any one side should be less than the sum of the other two sides. So here, the third side should be less than 22 + 14 = 36 cm.
• We know that in any triangle, any one side should be greater than the difference between the other two sides. So here, the third side side should be greater than 22 - 14 = 8 cm.
• Thus we can say, the length of the third side should fall between 8 cm and 36 cm
Solved example 9.12
Lengths of two sides of a triangle are 6 cm and 12 cm. Then between which two numbers should the third side fall?
Solution:
• The lengths of two sides are given as 6 and 12 cm
• We know that in any triangle, any one side should be less than the sum of the other two sides. So here, the third side should be less than 6 + 12 = 18 cm.
• We know that in any triangle, any one side should be greater than the difference between the other two sides. So here, the third side side should be greater than 12 - 6 = 6 cm.
• Thus we can say, the length of the third side should fall between 18 cm and 6 cm
A graphical representation of the answers of the above two problems are shown below:
 |
| Fig.9.19 Lengths shown in Blue colour are not allowed |
Solved example 9.13
In the triangle ABC shown in fig.9.20(a) below, prove that BC < OB + OC
 |
| Fig.9.20 |
• In the given triangle ABC, we can think of a smaller triangle BCO inside ABC.
• In this smaller triangle, if we take out BC, the other two sides are OB and OC.
• So one side is BC, and the other two sides are OB and OC.
• We know that any one side should be less than the sum of the other two sides.
• So we can write: BC < OB + OC
• In a similar way, we can prove:
AC < OA + OC and AB < OA + OB
Solved example 9.14
In the Δ PQR, a median RM is drawn fig.9.20(b). Prove that the sum of the three sides of the Δ PQR is greater than the median RM
Solution:
We have to prove that PQ + PR + QR > 2 RM:
• In Δ PRM, PM + PR > RM
• In Δ QRM, QR + QM > RM
• Adding the above two, we get: PM + PR + QR + QM > RM + RM
⇒ PQ + PR + QR > 2 RM (∵ PM + QM = PQ)
In the next section we will learn about Pythagoras Theorem.


No comments:
Post a Comment