In the previous sections we tried to find the side of a square whose area is 2 sq.units. We used trial and error method, but could not get an exact answer. Now we will try to use algebra.
1. In the previous section, we have seen that, the side would be a fraction. Because it lies in between 1 and 2
2. Let us assume that the fraction is x⁄y
3. Let us make one more assumption: That the fraction x⁄y is in it's lowest terms. That is., x and y do not have any common factor.
4. If the assumption in (3) is to be satisfied, the fraction should fall into any one of the following categories:
■ x is even, and, y is odd
■ x is odd and y is even
■ both x and y are odd
If we examine the above three categories, we will see that both x and y can not be even. If they are, (3) will not be satisfied. We can try several examples:
• 4⁄10 has even numbers in both numerator and denominator. It is not in it's lowest terms.
• 26⁄92 has even numbers in both numerator and denominator. It is not in it's lowest terms.
5. Now we can start the calculations. We have x⁄y as the side of our square. And our square has an area of 2 sq.units
6. So we can write: x⁄y × x⁄y = 2 ⇒ x2⁄y2 = 2 ⇒ x2 = 2y2
7. Look at the above result. x2 is equal to: (2 multiplied by y2)
Any quantity, which is 2 multiplied by some thing will be even. So x2 is even.
8. It follows that x is even.
This is based on the fact that: Square of an even number will be even, and, square of an odd number will be odd.
Some examples: • 22 = 4, • 52 = 25, • 142 = 196, • 92 = 81 etc.,
So we make an important conclusion: x is even
9. When x is even, it will be 2 times 'some thing'. Let 'k' be this 'some thing'. So we can write:
x = 2k. We do not have to worry about the value of k. It does not have much influence in our calculations.
10. Let us put x = 2k in our original equation which is: x2⁄y2 = 2. We get:
(2k)2⁄y2 = 2 ⇒ 4k2⁄y2 = 2 ⇒ y2 = 4k2⁄2 ⇒ y2 = 2k2
11. So now we find that y2 is 2 times 'some thing'. That is., y2 is even, and so y is even.
12. Here we find a contradiction: In (4) we said that one of x or y must be odd, and the other must be even. But now we find that both x [from (8)] and y [from (11)] are even.
13. So it can be concluded that, there is no fraction, which when squared, shall give us '2'.
Let us analyse the above result in (13):
• We want to draw a square with an exact area of 2 sq. units
• Any square can be drawn if length of it's side is known
• So if we know the 'appropriate length', we can draw the square with 2 sq.units area also
• But this 'appropriate length' can not be expressed in the form of a fraction x⁄y
• If it can not be expressed as x⁄y, it is not a rational number
• We call such numbers irrationals
How do we denote this 'appropriate length'? Let us try:
• We know that, length of the side of a square with area 4 sq.units is √4 = 2
• We know that, length of the side of a square with area 2.25 sq.units is √2.25 = 1.5
• We know that, length of the side of a square with area 81 sq.units is √81 = 9
We can write any number of examples like the above. In a similar way, we can write:
• Length of the side of a square with area 2 sq.units is √2
But saying √2 is not good enough. If we want to draw such a square, we want to be able to measure it out from a ruler. We want to know how much this √2 is. Such a knowledge is necessary to make measurements.
We will now try to find the value of √2. That is., the side of a square, whose area is 2 sq.units.
• Earlier, while using trial and error method, we reached upto the point (see fig.16.3.c) where we concluded that √2 lies between 11⁄8 and 3⁄2.
• It is convenient to proceed with decimals. 11⁄8 is 1.375, and 3⁄2 is 1.5
• So √2 lies in between 1.375 and 1.5
• Let us try 1.4: square of 1.4 = 1.42 = 1.96. It is still lesser than 2. So √2 lies in between 1.4 and 1.5
• Now, to take values in between 1.4 and 1.5, we will have to consider the second place after the decimal point:
1.412 = 1.9881 and 1.422 = 2.0164. So √2 lies in between 1.41 and 1.42
• We have to take the third decimal place. The calculations are done using a spread sheet. It is shown in the fig.16.4 below:
• Look at the third row. square of 1.42 gives 2.0164, which is greater than 2. So 1.42 is unacceptable.
• The required value lies between 1.41 and 1.42
• For obtaining a value between 1.41 and 1.42, we must move into the third decimal place.
• So we try 1.411, 1.412, 1.413 etc.,
• At the eighth row, the square again jumps over 2. So 1.415 is unacceptable
• The required value lies between 1.414 and 1.415
• For obtaining a value between 1.414 and 1.415, we must move into the fourth decimal place.
• So we try 1.4141, 1.4142, 1.413 etc.,
• At the eleventh row, the square again jumps over 2. So 1.4143 is unacceptable
• The required value lies between 1.4142 and 1.4143
• For obtaining a value between 1.4142 and 1.4143, we must move into the fifth decimal place.
• So we try 1.41421, 1.41422, 1.41423 etc.,
• At the thirteenth row, the square again jumps over 2. So 1.41422 is unacceptable
• The required value lies between 1.41421 and 1.41422
• For obtaining a value between 1.41421 and 1.41422, we must move into the sixth decimal place.
• So we try 1.414211, 1.414212, 1.414213 etc.,
• At the seventeenth row, the square again jumps over 2. So 1.414214 is unacceptable
• The required value lies between 1.414213 and 1.414214
So we have worked upto the sixth decimal place. But there is still no sign of getting an 'exact 2'. The fact is that, we will never get the 'exact 2', even if we go to thousands of decimal places. It is a non terminating decimal. But the square gets closer and closer to 2. This fact can be seen from the increasing number of 'nines' just after the decimal place.
We have learned about recurring decimals in a previous chapter. There we saw that:
• A single digit repeats for ever. OR
• A pattern repeats for ever
But what we have now is some thing different. There is no repetition of a single digit or a pattern. The digits will all be different. And, we will get a never ending number of decimal places.
However, we need not worry about it. There are strict rules in various fields of science and engineering, that tells us how many decimals places are to be considered. For example, if we want a square of area 2 sq.meters, we have the following options:
• If we take the length of side to be 1.41 m, that length will be correct to one centimetre. Because, 1.41 m = 141 centimetre
• If we take the length of side to be 1.414 m, that length will be correct to one millimetre. Because, 1.414 m = 1414 millimetre
We write: • √2 ≈ 1.4 (correct to 1 decimal place)
• √2 ≈ 1.41 (correct to 2 decimal places)
• √2 ≈ 1.414 (correct to 3 decimal places) and so on...
The symbol '≈' is read as 'almost equal to'.
For precise scientific and engineering works, more decimal places will be required. Any way, it is comforting to know that, when the decimal places in 1.414... increases, it's square gets closer and closer to '2'. Even though, we will never get exact '2'.
So we have seen that √2 is the length of the side of a square, whose area is 2 sq.m. There is another situation where we will encounter this √2. Consider the fig.16.5(a) below:
• ABC is a right triangle, right angled at A.
• AB and AC are the perpendicular sides. Length of both the perpendicular sides is 1 unit
• BC is the hypotenuse. What is the length of BC?
• Applying Pythagoras theorem, we get: BC2 = AB2 + AC2 ⇒ BC2 = 12 + 12 ⇒ BC2 = 1 + 1 ⇒ BC2 = 2. ∴ BC = √2
• So we find that, the hypotenuse of a right triangle, whose perpendicular sides are 1 unit each, is equal to √2
• Using the same calculations we will find that the diagonal of a square of side 1 unit is equal to √2. This is shown in fig.16.5(b)
So let us write a summary:
■ Length of the side of a square, whose area is 2 sq.m, is equal to √2
■ Hypotenuse of a right triangle, whose perpendicular sides are 1 unit each, is equal to √2
■ Diagonal of a square of side 1 unit is equal to √2
Fig.16.6 shows the same number line in fig.16.3.c. The extra modifications done are:
• The origin is marked as A, and the point of 1 unit is marked as B
• A perpendicular of 1 unit is erected at B. This perpendicular is named as BC. The points A and C are joined
• Now we have a right triangle ABC, right angled at B. AC is the hypotenuse
• Applying Pythagoras theorem, we get: AC2 = AB2 + BC2 ⇒ AC2 = 12 + 12 ⇒ AC2 = 1 + 1 ⇒ AC2 = 2. ∴ AC = √2
• This AC that we got, is in a sloping position. We want to transfer it onto the number line
• For that, with A as center, draw an arc with AC as radius
• This arc will cut the number line at a certain point. Mark this point as 'P'
• This 'P' is at the distance √2 from the origin. So 'P' is the representation of √2 on the number line
• Note that 'P' falls between 11⁄8 and 3⁄2, as expected
So we have seen the details about √2. In the next section, we will see √3.
1. In the previous section, we have seen that, the side would be a fraction. Because it lies in between 1 and 2
2. Let us assume that the fraction is x⁄y
3. Let us make one more assumption: That the fraction x⁄y is in it's lowest terms. That is., x and y do not have any common factor.
4. If the assumption in (3) is to be satisfied, the fraction should fall into any one of the following categories:
■ x is even, and, y is odd
■ x is odd and y is even
■ both x and y are odd
If we examine the above three categories, we will see that both x and y can not be even. If they are, (3) will not be satisfied. We can try several examples:
• 4⁄10 has even numbers in both numerator and denominator. It is not in it's lowest terms.
• 26⁄92 has even numbers in both numerator and denominator. It is not in it's lowest terms.
5. Now we can start the calculations. We have x⁄y as the side of our square. And our square has an area of 2 sq.units
6. So we can write: x⁄y × x⁄y = 2 ⇒ x2⁄y2 = 2 ⇒ x2 = 2y2
7. Look at the above result. x2 is equal to: (2 multiplied by y2)
Any quantity, which is 2 multiplied by some thing will be even. So x2 is even.
8. It follows that x is even.
This is based on the fact that: Square of an even number will be even, and, square of an odd number will be odd.
Some examples: • 22 = 4, • 52 = 25, • 142 = 196, • 92 = 81 etc.,
So we make an important conclusion: x is even
9. When x is even, it will be 2 times 'some thing'. Let 'k' be this 'some thing'. So we can write:
x = 2k. We do not have to worry about the value of k. It does not have much influence in our calculations.
10. Let us put x = 2k in our original equation which is: x2⁄y2 = 2. We get:
(2k)2⁄y2 = 2 ⇒ 4k2⁄y2 = 2 ⇒ y2 = 4k2⁄2 ⇒ y2 = 2k2
11. So now we find that y2 is 2 times 'some thing'. That is., y2 is even, and so y is even.
12. Here we find a contradiction: In (4) we said that one of x or y must be odd, and the other must be even. But now we find that both x [from (8)] and y [from (11)] are even.
13. So it can be concluded that, there is no fraction, which when squared, shall give us '2'.
Let us analyse the above result in (13):
• We want to draw a square with an exact area of 2 sq. units
• Any square can be drawn if length of it's side is known
• So if we know the 'appropriate length', we can draw the square with 2 sq.units area also
• But this 'appropriate length' can not be expressed in the form of a fraction x⁄y
• If it can not be expressed as x⁄y, it is not a rational number
• We call such numbers irrationals
How do we denote this 'appropriate length'? Let us try:
• We know that, length of the side of a square with area 4 sq.units is √4 = 2
• We know that, length of the side of a square with area 2.25 sq.units is √2.25 = 1.5
• We know that, length of the side of a square with area 81 sq.units is √81 = 9
We can write any number of examples like the above. In a similar way, we can write:
• Length of the side of a square with area 2 sq.units is √2
But saying √2 is not good enough. If we want to draw such a square, we want to be able to measure it out from a ruler. We want to know how much this √2 is. Such a knowledge is necessary to make measurements.
We will now try to find the value of √2. That is., the side of a square, whose area is 2 sq.units.
• Earlier, while using trial and error method, we reached upto the point (see fig.16.3.c) where we concluded that √2 lies between 11⁄8 and 3⁄2.
• It is convenient to proceed with decimals. 11⁄8 is 1.375, and 3⁄2 is 1.5
• So √2 lies in between 1.375 and 1.5
• Let us try 1.4: square of 1.4 = 1.42 = 1.96. It is still lesser than 2. So √2 lies in between 1.4 and 1.5
• Now, to take values in between 1.4 and 1.5, we will have to consider the second place after the decimal point:
1.412 = 1.9881 and 1.422 = 2.0164. So √2 lies in between 1.41 and 1.42
• We have to take the third decimal place. The calculations are done using a spread sheet. It is shown in the fig.16.4 below:
 |
| Fig.16.4 |
• The required value lies between 1.41 and 1.42
• For obtaining a value between 1.41 and 1.42, we must move into the third decimal place.
• So we try 1.411, 1.412, 1.413 etc.,
• At the eighth row, the square again jumps over 2. So 1.415 is unacceptable
• The required value lies between 1.414 and 1.415
• For obtaining a value between 1.414 and 1.415, we must move into the fourth decimal place.
• So we try 1.4141, 1.4142, 1.413 etc.,
• At the eleventh row, the square again jumps over 2. So 1.4143 is unacceptable
• The required value lies between 1.4142 and 1.4143
• For obtaining a value between 1.4142 and 1.4143, we must move into the fifth decimal place.
• So we try 1.41421, 1.41422, 1.41423 etc.,
• At the thirteenth row, the square again jumps over 2. So 1.41422 is unacceptable
• The required value lies between 1.41421 and 1.41422
• For obtaining a value between 1.41421 and 1.41422, we must move into the sixth decimal place.
• So we try 1.414211, 1.414212, 1.414213 etc.,
• At the seventeenth row, the square again jumps over 2. So 1.414214 is unacceptable
• The required value lies between 1.414213 and 1.414214
So we have worked upto the sixth decimal place. But there is still no sign of getting an 'exact 2'. The fact is that, we will never get the 'exact 2', even if we go to thousands of decimal places. It is a non terminating decimal. But the square gets closer and closer to 2. This fact can be seen from the increasing number of 'nines' just after the decimal place.
We have learned about recurring decimals in a previous chapter. There we saw that:
• A single digit repeats for ever. OR
• A pattern repeats for ever
But what we have now is some thing different. There is no repetition of a single digit or a pattern. The digits will all be different. And, we will get a never ending number of decimal places.
However, we need not worry about it. There are strict rules in various fields of science and engineering, that tells us how many decimals places are to be considered. For example, if we want a square of area 2 sq.meters, we have the following options:
• If we take the length of side to be 1.41 m, that length will be correct to one centimetre. Because, 1.41 m = 141 centimetre
• If we take the length of side to be 1.414 m, that length will be correct to one millimetre. Because, 1.414 m = 1414 millimetre
We write: • √2 ≈ 1.4 (correct to 1 decimal place)
• √2 ≈ 1.41 (correct to 2 decimal places)
• √2 ≈ 1.414 (correct to 3 decimal places) and so on...
The symbol '≈' is read as 'almost equal to'.
For precise scientific and engineering works, more decimal places will be required. Any way, it is comforting to know that, when the decimal places in 1.414... increases, it's square gets closer and closer to '2'. Even though, we will never get exact '2'.
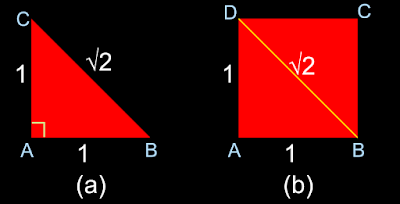 |
| Fig.16.5 |
• AB and AC are the perpendicular sides. Length of both the perpendicular sides is 1 unit
• BC is the hypotenuse. What is the length of BC?
• Applying Pythagoras theorem, we get: BC2 = AB2 + AC2 ⇒ BC2 = 12 + 12 ⇒ BC2 = 1 + 1 ⇒ BC2 = 2. ∴ BC = √2
• So we find that, the hypotenuse of a right triangle, whose perpendicular sides are 1 unit each, is equal to √2
• Using the same calculations we will find that the diagonal of a square of side 1 unit is equal to √2. This is shown in fig.16.5(b)
So let us write a summary:
■ Length of the side of a square, whose area is 2 sq.m, is equal to √2
■ Hypotenuse of a right triangle, whose perpendicular sides are 1 unit each, is equal to √2
■ Diagonal of a square of side 1 unit is equal to √2
 |
| Fig.16.6 |
• The origin is marked as A, and the point of 1 unit is marked as B
• A perpendicular of 1 unit is erected at B. This perpendicular is named as BC. The points A and C are joined
• Now we have a right triangle ABC, right angled at B. AC is the hypotenuse
• Applying Pythagoras theorem, we get: AC2 = AB2 + BC2 ⇒ AC2 = 12 + 12 ⇒ AC2 = 1 + 1 ⇒ AC2 = 2. ∴ AC = √2
• This AC that we got, is in a sloping position. We want to transfer it onto the number line
• For that, with A as center, draw an arc with AC as radius
• This arc will cut the number line at a certain point. Mark this point as 'P'
• This 'P' is at the distance √2 from the origin. So 'P' is the representation of √2 on the number line
• Note that 'P' falls between 11⁄8 and 3⁄2, as expected
No comments:
Post a Comment