In the previous section we saw the method to draw an equilateral triangle inside a circle. In this section, we will see some solved examples.
Solved example 17.1
Fig.17.7(a) below shows two circles
centred on the same point, and a line intersecting them.
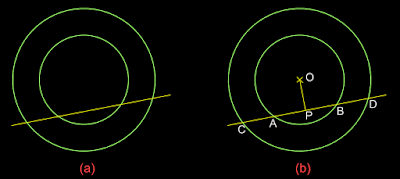 |
| Fig.17.7 |
Prove that
the parts of the line between the circles on either side are equal.
Solution:
1. In the fig.17.7(a), we have
two circles. The centres of both the circles are the same. But the diameters are different. Such
circles are called ‘concentric circles’.
2. A straight line cuts through both the
circles. It becomes a chord for both the circles. This is shown in
fig.b. We have to prove that DB = CA
3. AB is a chord for the inner
circle, and CD is a chord for the outer circle.
4. Let O be the centre of the
circle. A perpendicular is drawn from O to the cutting line.
5. According to theorem 17.1,
such a perpendicular will bisect the chord. So we get:
6. AP = BP (considering the
inner circle) AND
7. CP = DP (considering the
outer circle)
8. Also we can write: CA = CP
– AP AND
9. DB = DP – BP
10. From (7) we get DP = CP, AND
from (6) we get BP = AP.
11. Substituting these values in
(9) we get: DB = CP – AP.
12. But in (8), we have CP – AP = CA. So we get DB = CA
■ The above steps can be
literally written as follows:
• CP is equal to DP
♦ If we take away a quantity AP
from CP, we will get CA
♦ If we take away a quantity BP
from DP, we will get DB
• But AP = BP. So the quantity
that will remain after the ‘take away’ will be same on both
sides. That is., DB will be equal to CA
Solved example 17.2
Prove that the line joining the centres of two intersecting circles is the perpendicular bisector of the line joining the points of intersection
Solution:
• In the fig.17.8(a), PQ is the line joining the centres of the two intersecting circles
• MN is the line joining the points of intersection
 |
| Fig.17.8 |
• We have to prove two things:
♦ PQ is perpendicular to MN
♦ PQ bisects MN
■ In other words, we have to prove that, PQ is the perpendicular bisector of MN. The steps are as follows:
1. In fig.17.7(b), 4 extra lines are drawn. They are: PN, QN, PM, and QM.
2. When we draw those lines, we get some new triangles
3. Consider the two triangles: ΔPMQ and ΔPNQ
4. PM = PN (∵ radii of the same circle)
5. QM = QN (∵ radii of the same circle)
6. PQ = PQ
7. From the above 3 steps, it is cler that all the sides present in ΔPMQ is present in ΔPNQ also. It is a case of SSS congruence
8. Let us write the correspondence:
9. P↔P, Q↔Q and M↔N. From this we can write:
10. From P↔P, we can write: The angle at P in ΔPMQ is equal to the angle at P in ΔPNQ. That is., ∠MPQ = ∠NPQ
11. Now consider another pair of triangles: ΔMPX and ΔNPX
12. MP = NP (∵ radii of the same circle)
13. PX = PX
14. ∠MPQ = ∠NPQ [from (10)]
15. So two sides and their included angle is same in both the triangles. It is a case of SAS congruence. Let us write the correspondence:
16. P↔P, X↔X and M↔N. From this we can write:
17. PX↔PX, PM↔PN, MX↔MN.
18. From MX↔MN we can write: MX is equal to MN. This is one of the results that we have to obtain. When MX = MN, it is clear that, PQ bisects MN.
19. Now all that remains to be proven is that PQ is perpendicular to MN. Let us continue:
20. In (16) we obtained X↔X. So the angle at X is equal in the two triangles ΔMPX and ΔNPX . That means ∠MXP = ∠NXP
20. In (16) we obtained X↔X. So the angle at X is equal in the two triangles ΔMPX and ΔNPX . That means ∠MXP = ∠NXP
21. As these two angles are equal, we will put each equal to ‘k’. So the sum of the two angles = k + k = 2k
22. But the sum of these angles will be 180o. (∵they form a linear pair). So we can write 2k = 180o. Thus k = 90o.
23. That is., ∠MXP = ∠NXP = 90o. This means PQ is perpendicular to MN
■ So the calculation steps are complete. We take (18) and (23). The results in those two steps prove that PQ is the perpendicular bisector of MN
Solved example 17.3
A chord and a diameter through
one of it's ends are drawn in a circle. Another chord of same inclination
is drawn on the other side of the diameter. See fig.17.9(a) below.
 |
| Fig.17.9 |
Prove that the chords are
of the same length.
Solution:
• In fig.17.9(b), the first chord is
marked as AB.
• For a circle, any number of
diameters can be drawn. Only condition is that they must all pass
through the centre of the circle.
• In this problem, the diameter
AD passes through the centre, as well as the end point 'A' of the
chord.
• Another chord AC is also
drawn. It's inclination towards the diameter AD is same as the
inclination of AB towards AD
• Let the inclination be equal
to 'k' degrees.
• Draw OB and OC
Now we can begin the
calculations:
1. Consider ΔOAB. We have OA
= OB (∵ radii of the same circle)
2. So it is an isosceles
triangle, and the base angles will be equal.
3. Thus we get ∠OAB = ∠OBA
= k
4. We can write: k + k + ∠AOB
= 180o (sum of interior angles of a triangle is 180o.)
⇒ 2k + ∠AOB = 180 ⇒ AOB = (180 – 2k)
5. We can do the same steps
from (1) to (4) for the other ΔOAC and obtain ∠AOC = (180 – 2k)
6. Now consider the two
triangles: ΔAOB and ΔAOC
♦ OA = OA ♦ OB = OC (∵ radii of the
same circle)
♦ From (4) and (5), we have
∠AOB = ∠AOC = (180 – 2k)
7. So we have two sides and the
included angle same in the two triangles. It is an SAS congruence.
The two triangles are equal.
8. Let us write the
correspondence: O↔O, A↔A and B↔C
9. From A↔A and B↔C, we get AB = AC (see
fig.17.9.c)
Solved example 17.4
Prove that the angle between
two equal chords drawn from a point is bisected by the diameter
through that point
Solution:
• In fig.17.10, the first chord is
marked as AB. The second chord is marked as AC. Given that AB = AC
 |
| Fig.17.10 |
• For a circle, any number of
diameters can be drawn. Only condition is that they must all pass
through the centre of the circle.
• In this problem, the diameter
AD passes through the centre, as well as the point of intersection
'A' of the chords.
• The diameter AD splits ∠CAB
into 2 smaller angles: ∠CAO (denoted as 'x') and ∠BAO (denoted as
'y')
We have to prove that the
diameter bisects the angle at A. That is., we have to prove x = y
• Draw OB and OC. Now we can begin the
calculations:
1. Consider ΔOAB and ΔOAC
♦ OA = OA ♦ OB = OC (∵
radii of the same circle) ♦ AB = AC (given)
2. So it is a case of SSS
congruence. Let us write the correspondence:
O↔O, A↔A and B↔C
3. We have A↔A . So the angles
at A are equal. That is., ∠BAO = ∠CAO same as x = y
No comments:
Post a Comment