In the previous section we saw solved examples which demonstrate the expression of distance as absolute value. In this section we will see a few more solved examples.
Solved example 22.10
Find the solutions to the equation: |x-1| = |x-3|
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 1
3. We have a point C on the number line. The number corresponding to the point C is 3
4. The difference between the numbers corresponding to A and B = (x-1)
5. Applying theorem 22.5, the distance between A and B is |(x-1)|
6. The difference between the numbers corresponding to A and C = (x-3)
7. Applying theorem 22.5, the distance between A and B is |(x-3)|
8. But these distances are given as equal.
9. That means the distance from B to A is same as the distance from C to A. Now look at the number line in fig.22.26 below:
10. If the distance from B toA is same as the distance from C to A, there is only one possibility:
• A is the midpoint between B and C
11. So we are in the following situation:
• We have a point B, whose number is known
• We have a point C, whose number is known
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and C
12. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and C = 1+3 = 4
• Number corresponding to the midpoint A = Half of the sum = 4/2 = 2
Thus we get x = 2
13. Check: |x-1| = |x-3| ⇒ |2-1| = |2-3| ⇒ |1| = |-1| ⇒ 1 = 1 Which is true
Solved example 22.11
Find the solutions to the equation: |x-3| = |x-4|
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 3
3. We have a point C on the number line. The number corresponding to the point C is 4
4. The difference between the numbers corresponding to A and B = (x-3)
5. Applying theorem 22.5, the distance between A and B is |(x-3)|
6. The difference between the numbers corresponding to A and C = (x-4)
7. Applying theorem 22.5, the distance between A and B is |(x-4)|
8. But these distances are given as equal.
9. That means, the distance from B to A is same as the distance from C to A. Now look at the number line in fig.22.27 below:
10. If the distance from B to A is same as the distance from C to A, there is only one possibility:
• A is the midpoint between B and C
11. So we are in the following situation:
• We have a point B, whose number is known
• We have a point C, whose number is known
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and C
12. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and C = 3+4 = 7
• Number corresponding to the midpoint A = Half of the sum = 7/2 = 3.5
Thus we get x = 3.5
13. Check: |x-3| = |x-4| ⇒ |3.5-3| = |3.5-4| ⇒ |0.5| = |-0.5| ⇒ 0.5 = 0.5 Which is true
Solved example 22.12
Find the solutions to the equation: |x+2| = |x-5|
Solution:
• (x+2) can be modified as [x-(-2)]. So we can write the steps as follows:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is -2
3. We have a point C on the number line. The number corresponding to the point C is 5
4. The difference between the numbers corresponding to A and B = [x-(-2)]
5. Applying theorem 22.5, the distance between A and B is |[x-(-2)]|
6. The difference between the numbers corresponding to A and C = (x-5)
7. Applying theorem 22.5, the distance between A and B is |(x-5)|
8. But these distances are given as equal.
9. That means, the distance from B to A is same as the distance from C to A. Now look at the number line in fig.22.27 below:
10. If the distance from B to A is same as the distance from C to A, there is only one possibility:
• A is the midpoint between B and C
11. So we are in the following situation:
• We have a point B, whose number is known
• We have a point C, whose number is known
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and C
12. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and C = -2+5 = 3
• Number corresponding to the midpoint A = Half of the sum = 3/2 = 1.5
Thus we get x = 1.5
13. Check: |x+2| = |x-5| ⇒ |1.5+2| = |1.5-5| ⇒ |3.5| = |-3.5| ⇒ 3.5 = 3.5 Which is true
Solved example 22.13
Find the solutions to the equation: |x| = |x+1|
Solution:
• |x| is the distance of the 'point whose number is x' from zero
• (x+1) can be modified as [x-(-1)].
So we can write the steps as follows:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is -1
3. The distance of A from zero is |x|
4. The difference between the numbers corresponding to A and B = [x-(-1)]
5. Applying theorem 22.5, the distance between A and B is | [x-(-1)]|
6. But these distances are given as equal.
7. That means, the distance from B to A is same as the distance from A to zero. Now look at the number line in fig.22.28 below:
8. If the distance from B to A is same as the distance from A to zero, there is only one possibility:
• A is the midpoint between B and zero
9. So we are in the following situation:
• We have a point B, whose number is known
• We have the point zero, whose number is '0'
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and zero
10. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and zero = -1+0 = -1
• Number corresponding to the midpoint A = Half of the sum = -1/2 = -0.5
Thus we get x = -0.5
11. Check: |x| = |x+1| ⇒ |-0.5| = |-0.5+1| ⇒ |-0.5| = |0.5| ⇒ 0.5 = 0.5 Which is true
Alternate method:
• x can be modified as (x-0)
• (x+1) can be modified as [x-(-1)].
So we can write the steps as follows:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 0
3. We have a point C on the number line. The number corresponding to the point C is -1
4. The difference between the numbers corresponding to A and B = (x-0)
5. Applying theorem 22.5, the distance between A and B is |(x-0)|
6. The difference between the numbers corresponding to A and C = [x-(-1)]
7. Applying theorem 22.5, the distance between A and B is | [x-(-1)]|
8. But these distances are given as equal.
9. That means, the distance from B to A is same as the distance from C to A. Now look at the number line in fig.22.29 below:
10. If the distance from B to A is same as the distance from C to A, there is only one possibility:
• A is the midpoint between B and C
11. So we are in the following situation:
• We have a point B, whose number is known
• We have a point C, whose number is known
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and C
12. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and C = -1+0 = -1
• Number corresponding to the midpoint A = Half of the sum = -1/2 = -0.5
Thus we get x = -0.5
13. Check: |x| = |x+1| ⇒ |-0.5| = |-0.5+1| ⇒ |-0.5| = |0.5| ⇒ 0.5 = 0.5 Which is true
Solved example 22.14
Prove that if 1 < x < 4 and 1 < y < 4, then |x-y| < 3
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 1
3. We have a point C on the number line. The number corresponding to the point C is 4
4. We have a point D on the number line. The number corresponding to the point D is y
5. Given that 1 < x < 4. So the point A can be any where in between C and D
x can never take a value of exact 1 or exact 4. So hollow circles are shown at B and C in the graph below:
6. Given that 1 < y < 4. So the point D can be any where in between B and C
y can never take a value of exact 1 or exact 4.
7. We want the difference between x and y. The 'maximum difference' will be obtained in the following situation:
• When one of them (x or y) is at it's maximum possible value AND
• The other is at it's minimum possible value
8. When one of them is at it's maximum possible value, it will be 'just to the left of 4'
Then the other is at the minimum possible value, which is 'just to the right of 1'
9. Concentrate on the two positions:
• One point is 'just to the left of 4'
• The other point is 'just to the right of 1'
10. In such a situation, the distance between them (calculated as |x-y|) will be less than 3
■ We will get 3 only if one is at 'exact 4' and the other is at 'exact 1'
11. Thus we find that the maximum possible distance is less than 3
We can write: |x-y| < 3
Solved example 22.15
Prove that if x < 3 and y > 7, then |x-y| > 4
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 3
3. We have a point C on the number line. The number corresponding to the point C is 7
4. We have a point D on the number line. The number corresponding to the point D is y
5. Given that x < 3. So the point A can be any where on the red line
x can never take a value of exact 3. So hollow circle is shown at B in the graph below:
6. Given that y > 7. So the point D can be any where on the blue line
y can never take a value of exact 7.
7. We want the difference between x and y. The 'minimum difference' will be obtained in the following situation:
• When x is just to the left of B AND
• y is just to the right of C
• If any one of them is at a different position other than the above two, the difference will not be minimum
8. Concentrate on the two positions:
• x is 'just to the left of B'
• y is 'just to the right of C'
10. In such a situation, the distance between them (calculated as |x-y|) will be greater than 4
■ We will get 4 only if x is at 'exact 3' and y is at 'exact 7'
11. Thus we find that the minimum possible distance is greater than 4
We can write: |x-y| > 4
Solved example 22.16
What are the numbers x, for which |x-2| + |x-8| = 6
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 2
3. We have a point C on the number line. The number corresponding to the point C is 8
4. The difference between the numbers corresponding to A and B = (x-2)
5. Applying theorem 22.5, the distance between A and B is |x-2|
6. The difference between the numbers corresponding to A and C = (x-8)
7. Applying theorem 22.5, the distance between A and B is |x-8|
8. The sum of the two distances is given as 6. Consider the number line shown in fig.21.32 below:
9. We can see that the actual distance between B and C is (8-2) = 6 units
10. So A can lie anywhere on the red line. It can also take the exact values 2 and 8
11. So we can write 2 ≤ x ≤ 8
12. Check: • Let x = 2
Then |x-2| + |x-8| = 6 ⇒|2-2| + |2-8| = 6 ⇒ |0| + |-6| = 6 ⇒ 0 + 6 = 6 ⇒6 = 6 which is true
• Let x = 4
Then |x-2| + |x-8| = 6 ⇒|4-2| + |4-8| = 6 ⇒ |2| + |-4| = 6 ⇒ 2 + 4 = 6 ⇒6 = 6 which is true
• Let x = 8
Then |x-2| + |x-8| = 6 ⇒|8-2| + |8-8| = 6 ⇒ |6| + |0| = 6 ⇒ 6 + 0 = 6 ⇒6 = 6 which is true
Solved example 22.17
What are the numbers x, for which |x-2| + |x-8| = 10
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 2
3. We have a point C on the number line. The number corresponding to the point C is 8
4. The difference between the numbers corresponding to A and B = (x-2)
5. Applying theorem 22.5, the distance between A and B is |x-2|
6. The difference between the numbers corresponding to A and C = (x-8)
7. Applying theorem 22.5, the distance between A and B is |x-8|
8. The sum of the two distances is given as 10. Consider the number line shown in fig.21.33 below:
9. The two possible positions of A are shown in blue colour. The corresponding numbers are 0 and 10
10. Check: • Let x = 0
Then |x-2| + |x-8| = 10 ⇒|0-2| + |0-8| = 10 ⇒ |-2| + |-8| = 10 ⇒ 2 + 8 = 10 ⇒10 = 10 which is true
• Let x = 10
Then |x-2| + |x-8| = 10 ⇒|10-2| + |10-8| = 10 ⇒ |8| + |2| = 10 ⇒ 8 + 2 = 10 ⇒10 = 10 which is true
Another method:
We will consider all the possible values that x can take.
Case 1: x < 2
1. Then (x-2) will be a negative quantity. This is same as (2-x) is a positive quantity
2. Whether we take (x-2) or (2-x), both are 'difference'. And when we take the absolute value, we are dropping the '-' sign.
3. So, when x < 2, |x-2| = (2-x)
4. When x is less than 2, it will be less than 8 also. So |x-8| = (8-x)
5. Substituting these values in the given equation we get:
(2-x) + (8-x) = 10 ⇒ 10 -2x = 10 ⇒ 2x = 0 ⇒ x = 0
Case 2: x = 2
1. Then (x-2) = 0 and |0| = 0
2. |x-8| = |(2-8)| = |-6| = 6
3. Substituting these values in the given equation we get:
0 + 6 = 10. This is not true. So we cannot consider case 2
Case 3: x > 2 AND x < 8
1. That means x is greater than 2, but at the same time, x is less than 8
2. Another way of writing this is: 2 < x < 8
3. Graphically, this will be a line from 2 to 8, with hollow circles at 2 and 8
4. Let us see whether any of such values of x satisfies the given equation:
5. When x > 2, (x-2) is positive. So |x-2| = (x-2)
6. When x is less than 8, (x-8) is negative. So |x-8| = (8-x)
7. Substituting these values in the given equation we get:
(x-2) + (8-x) = 10 ⇒ 6 = 10. This is not true. So we cannot consider case 3
Case 4: x = 8
1. Then (x-2) = 6 and |6| = 6
2. |x-8| = 0 and |0| = 0
3. Substituting these values in the given equation we get:
6 + 0 = 10. This is not true. So we cannot consider case 4
Case 5: x > 8
1. Then x will be greater than 2 also. So |x-2| = (x-2)
2. (x-8) will be positive. So |x-8| = (x-8)
3. Substituting these values in the given equation we get:
4. (x-2) + (x-8) = 10 ⇒ 2x-10 = 10 ⇒ 2x = 20 ⇒ x = 10
■ So we considered 5 cases. Those 5 cases cover all possible numbers on the number line. But only the cases 1 and 5 will give us a valid result.
• The valid results are: x = 0 and x = 10
Solved example 22.10
Find the solutions to the equation: |x-1| = |x-3|
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 1
3. We have a point C on the number line. The number corresponding to the point C is 3
4. The difference between the numbers corresponding to A and B = (x-1)
5. Applying theorem 22.5, the distance between A and B is |(x-1)|
6. The difference between the numbers corresponding to A and C = (x-3)
7. Applying theorem 22.5, the distance between A and B is |(x-3)|
8. But these distances are given as equal.
9. That means the distance from B to A is same as the distance from C to A. Now look at the number line in fig.22.26 below:
 |
| Fig.22.26 |
• A is the midpoint between B and C
11. So we are in the following situation:
• We have a point B, whose number is known
• We have a point C, whose number is known
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and C
12. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and C = 1+3 = 4
• Number corresponding to the midpoint A = Half of the sum = 4/2 = 2
Thus we get x = 2
13. Check: |x-1| = |x-3| ⇒ |2-1| = |2-3| ⇒ |1| = |-1| ⇒ 1 = 1 Which is true
Solved example 22.11
Find the solutions to the equation: |x-3| = |x-4|
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 3
3. We have a point C on the number line. The number corresponding to the point C is 4
4. The difference between the numbers corresponding to A and B = (x-3)
5. Applying theorem 22.5, the distance between A and B is |(x-3)|
6. The difference between the numbers corresponding to A and C = (x-4)
7. Applying theorem 22.5, the distance between A and B is |(x-4)|
8. But these distances are given as equal.
9. That means, the distance from B to A is same as the distance from C to A. Now look at the number line in fig.22.27 below:
 |
| Fig.22.27 |
• A is the midpoint between B and C
11. So we are in the following situation:
• We have a point B, whose number is known
• We have a point C, whose number is known
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and C
12. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and C = 3+4 = 7
• Number corresponding to the midpoint A = Half of the sum = 7/2 = 3.5
Thus we get x = 3.5
13. Check: |x-3| = |x-4| ⇒ |3.5-3| = |3.5-4| ⇒ |0.5| = |-0.5| ⇒ 0.5 = 0.5 Which is true
Solved example 22.12
Find the solutions to the equation: |x+2| = |x-5|
Solution:
• (x+2) can be modified as [x-(-2)]. So we can write the steps as follows:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is -2
3. We have a point C on the number line. The number corresponding to the point C is 5
4. The difference between the numbers corresponding to A and B = [x-(-2)]
5. Applying theorem 22.5, the distance between A and B is |[x-(-2)]|
6. The difference between the numbers corresponding to A and C = (x-5)
7. Applying theorem 22.5, the distance between A and B is |(x-5)|
8. But these distances are given as equal.
9. That means, the distance from B to A is same as the distance from C to A. Now look at the number line in fig.22.27 below:
 |
| Fig.22.27 |
• A is the midpoint between B and C
11. So we are in the following situation:
• We have a point B, whose number is known
• We have a point C, whose number is known
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and C
12. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and C = -2+5 = 3
• Number corresponding to the midpoint A = Half of the sum = 3/2 = 1.5
Thus we get x = 1.5
13. Check: |x+2| = |x-5| ⇒ |1.5+2| = |1.5-5| ⇒ |3.5| = |-3.5| ⇒ 3.5 = 3.5 Which is true
Solved example 22.13
Find the solutions to the equation: |x| = |x+1|
Solution:
• |x| is the distance of the 'point whose number is x' from zero
• (x+1) can be modified as [x-(-1)].
So we can write the steps as follows:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is -1
3. The distance of A from zero is |x|
4. The difference between the numbers corresponding to A and B = [x-(-1)]
5. Applying theorem 22.5, the distance between A and B is | [x-(-1)]|
6. But these distances are given as equal.
7. That means, the distance from B to A is same as the distance from A to zero. Now look at the number line in fig.22.28 below:
 |
| Fig.22.28 |
• A is the midpoint between B and zero
9. So we are in the following situation:
• We have a point B, whose number is known
• We have the point zero, whose number is '0'
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and zero
10. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and zero = -1+0 = -1
• Number corresponding to the midpoint A = Half of the sum = -1/2 = -0.5
Thus we get x = -0.5
11. Check: |x| = |x+1| ⇒ |-0.5| = |-0.5+1| ⇒ |-0.5| = |0.5| ⇒ 0.5 = 0.5 Which is true
Alternate method:
• x can be modified as (x-0)
• (x+1) can be modified as [x-(-1)].
So we can write the steps as follows:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 0
3. We have a point C on the number line. The number corresponding to the point C is -1
4. The difference between the numbers corresponding to A and B = (x-0)
5. Applying theorem 22.5, the distance between A and B is |(x-0)|
6. The difference between the numbers corresponding to A and C = [x-(-1)]
7. Applying theorem 22.5, the distance between A and B is | [x-(-1)]|
8. But these distances are given as equal.
9. That means, the distance from B to A is same as the distance from C to A. Now look at the number line in fig.22.29 below:
 |
| Fig.22.29 |
• A is the midpoint between B and C
11. So we are in the following situation:
• We have a point B, whose number is known
• We have a point C, whose number is known
• We have a point A, whose number is not known. But we know that, A is the midpoint between B and C
12. In this situation, we apply theorem 22.3.
• Sum of the numbers corresponding to B and C = -1+0 = -1
• Number corresponding to the midpoint A = Half of the sum = -1/2 = -0.5
Thus we get x = -0.5
13. Check: |x| = |x+1| ⇒ |-0.5| = |-0.5+1| ⇒ |-0.5| = |0.5| ⇒ 0.5 = 0.5 Which is true
Solved example 22.14
Prove that if 1 < x < 4 and 1 < y < 4, then |x-y| < 3
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 1
3. We have a point C on the number line. The number corresponding to the point C is 4
4. We have a point D on the number line. The number corresponding to the point D is y
5. Given that 1 < x < 4. So the point A can be any where in between C and D
x can never take a value of exact 1 or exact 4. So hollow circles are shown at B and C in the graph below:
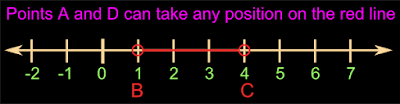 |
| Fig.22.30 |
y can never take a value of exact 1 or exact 4.
7. We want the difference between x and y. The 'maximum difference' will be obtained in the following situation:
• When one of them (x or y) is at it's maximum possible value AND
• The other is at it's minimum possible value
8. When one of them is at it's maximum possible value, it will be 'just to the left of 4'
Then the other is at the minimum possible value, which is 'just to the right of 1'
9. Concentrate on the two positions:
• One point is 'just to the left of 4'
• The other point is 'just to the right of 1'
10. In such a situation, the distance between them (calculated as |x-y|) will be less than 3
■ We will get 3 only if one is at 'exact 4' and the other is at 'exact 1'
11. Thus we find that the maximum possible distance is less than 3
We can write: |x-y| < 3
Solved example 22.15
Prove that if x < 3 and y > 7, then |x-y| > 4
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 3
3. We have a point C on the number line. The number corresponding to the point C is 7
4. We have a point D on the number line. The number corresponding to the point D is y
5. Given that x < 3. So the point A can be any where on the red line
x can never take a value of exact 3. So hollow circle is shown at B in the graph below:
 |
| Fig.22.31 |
y can never take a value of exact 7.
7. We want the difference between x and y. The 'minimum difference' will be obtained in the following situation:
• When x is just to the left of B AND
• y is just to the right of C
• If any one of them is at a different position other than the above two, the difference will not be minimum
8. Concentrate on the two positions:
• x is 'just to the left of B'
• y is 'just to the right of C'
10. In such a situation, the distance between them (calculated as |x-y|) will be greater than 4
■ We will get 4 only if x is at 'exact 3' and y is at 'exact 7'
11. Thus we find that the minimum possible distance is greater than 4
We can write: |x-y| > 4
Solved example 22.16
What are the numbers x, for which |x-2| + |x-8| = 6
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 2
3. We have a point C on the number line. The number corresponding to the point C is 8
4. The difference between the numbers corresponding to A and B = (x-2)
5. Applying theorem 22.5, the distance between A and B is |x-2|
6. The difference between the numbers corresponding to A and C = (x-8)
7. Applying theorem 22.5, the distance between A and B is |x-8|
8. The sum of the two distances is given as 6. Consider the number line shown in fig.21.32 below:
 |
| Fig.22.32 |
10. So A can lie anywhere on the red line. It can also take the exact values 2 and 8
11. So we can write 2 ≤ x ≤ 8
12. Check: • Let x = 2
Then |x-2| + |x-8| = 6 ⇒|2-2| + |2-8| = 6 ⇒ |0| + |-6| = 6 ⇒ 0 + 6 = 6 ⇒6 = 6 which is true
• Let x = 4
Then |x-2| + |x-8| = 6 ⇒|4-2| + |4-8| = 6 ⇒ |2| + |-4| = 6 ⇒ 2 + 4 = 6 ⇒6 = 6 which is true
• Let x = 8
Then |x-2| + |x-8| = 6 ⇒|8-2| + |8-8| = 6 ⇒ |6| + |0| = 6 ⇒ 6 + 0 = 6 ⇒6 = 6 which is true
Solved example 22.17
What are the numbers x, for which |x-2| + |x-8| = 10
Solution:
1. We have a point A on the number line. The number corresponding to the point A is x
2. We have a point B on the number line. The number corresponding to the point B is 2
3. We have a point C on the number line. The number corresponding to the point C is 8
4. The difference between the numbers corresponding to A and B = (x-2)
5. Applying theorem 22.5, the distance between A and B is |x-2|
6. The difference between the numbers corresponding to A and C = (x-8)
7. Applying theorem 22.5, the distance between A and B is |x-8|
8. The sum of the two distances is given as 10. Consider the number line shown in fig.21.33 below:
9. The two possible positions of A are shown in blue colour. The corresponding numbers are 0 and 10
10. Check: • Let x = 0
Then |x-2| + |x-8| = 10 ⇒|0-2| + |0-8| = 10 ⇒ |-2| + |-8| = 10 ⇒ 2 + 8 = 10 ⇒10 = 10 which is true
• Let x = 10
Then |x-2| + |x-8| = 10 ⇒|10-2| + |10-8| = 10 ⇒ |8| + |2| = 10 ⇒ 8 + 2 = 10 ⇒10 = 10 which is true
Another method:
We will consider all the possible values that x can take.
Case 1: x < 2
1. Then (x-2) will be a negative quantity. This is same as (2-x) is a positive quantity
2. Whether we take (x-2) or (2-x), both are 'difference'. And when we take the absolute value, we are dropping the '-' sign.
3. So, when x < 2, |x-2| = (2-x)
4. When x is less than 2, it will be less than 8 also. So |x-8| = (8-x)
5. Substituting these values in the given equation we get:
(2-x) + (8-x) = 10 ⇒ 10 -2x = 10 ⇒ 2x = 0 ⇒ x = 0
Case 2: x = 2
1. Then (x-2) = 0 and |0| = 0
2. |x-8| = |(2-8)| = |-6| = 6
3. Substituting these values in the given equation we get:
0 + 6 = 10. This is not true. So we cannot consider case 2
Case 3: x > 2 AND x < 8
1. That means x is greater than 2, but at the same time, x is less than 8
2. Another way of writing this is: 2 < x < 8
3. Graphically, this will be a line from 2 to 8, with hollow circles at 2 and 8
4. Let us see whether any of such values of x satisfies the given equation:
5. When x > 2, (x-2) is positive. So |x-2| = (x-2)
6. When x is less than 8, (x-8) is negative. So |x-8| = (8-x)
7. Substituting these values in the given equation we get:
(x-2) + (8-x) = 10 ⇒ 6 = 10. This is not true. So we cannot consider case 3
Case 4: x = 8
1. Then (x-2) = 6 and |6| = 6
2. |x-8| = 0 and |0| = 0
3. Substituting these values in the given equation we get:
6 + 0 = 10. This is not true. So we cannot consider case 4
Case 5: x > 8
1. Then x will be greater than 2 also. So |x-2| = (x-2)
2. (x-8) will be positive. So |x-8| = (x-8)
3. Substituting these values in the given equation we get:
4. (x-2) + (x-8) = 10 ⇒ 2x-10 = 10 ⇒ 2x = 20 ⇒ x = 10
■ So we considered 5 cases. Those 5 cases cover all possible numbers on the number line. But only the cases 1 and 5 will give us a valid result.
• The valid results are: x = 0 and x = 10

No comments:
Post a Comment