In the previous section we completed the discussion on Histograms. In this section we will see 'Frequency polygons'.
Let us revisit the first histogram that we saw in this chapter. It is given in fig.25.6. To this histogram, do the following modifications:
1. Mark the midpoints of the upper edges of all the rectangles
2. Name these midpoints as B, C, D, E, F and G
3. Join these midpoints by line segments
These line segments are shown in blue colour in the fig.25.15 below:
We have not obtained the polygon yet. For that we continue the modification steps
4. Assume that there is a class interval before 30.5-35.5
What will be the limits of such an interval?
Ans: We know that the width is 5
• So the lower limit of that interval will be 30.5-5 = 25.5
• Thus the lower limit is 25.5, and upper limit is 30.5
5. Assume that there is a class interval after before 55.5-60.5
What will be the limits of such an interval?
Ans: We know that the width is 5
• So the upper limit of that interval will be 60.5+5 = 65.5
• Thus the lower limit is 60.5, and upper limit is 65.5
6. Mark the midpoint of 25.5-30.5 as A
Mark the midpoint of 60.5-65.5 as H
7. Draw the line segments AB and GH. This is shown in fig. 25.16 below:
Now we have a polygon ABCDEFGH. It's base is AH. The base AH rests on the x-axis
This polygon ABCDEFGH has a peculiarity: It's area is same as the area of the histogram
Let us prove it:
1. In the fig.25.17 below, the line segment AB gives us two triangles. One at the top, and other at the bottom. They are shown in red colour.
2. Is there any relation between the two red triangles? Let us find out:
3. The two triangles are enlarged and shown at the side of the fig.25.17. The top triangle is named as PBR, and the bottom triangle is named as AQR
(i) Line PQ is the left edge of the first rectangle in the histogram.
(ii) AQ lies on the x-axis
(iii) PB lies on the top edge of the first rectangle of the histogram
From the above three points it is clear that:
• PQ is perpendicular to PB. So ∠P = 90o. It is shown in white colour in the top triangle
• PQ is perpendicular to AQ. So ∠Q = 90o. It is shown in white colour in the bottom triangle
4. PB and AQ are parallel. They are cut by a transversal AB. So ∠B = ∠A. They are shown in yellow colour
5. ∠R is same in both triangles because, they are opposite angles. They are shown in blue colour
6. Length of AQ = half of class-interval 25.5-30.5 = half of 5 = 2.5
Length of PB = half of class-interval 30.5-35.5 = half of 5 = 2.5
Thus we get AQ = PB
7. So we have the following situation:
• In the upper triangle, there is a length PB of 2.5 cm, with white and yellow angles at it's ends
• In the bottom triangle, there is a length AQ of 2.5 cm, with white and yellow angles at it's ends
• It is a case of ASA congruence. The two red triangles AQR and BPR are equal.
• The bottom red triangle is outside the histogram but it is inside the polygon
■ So, while calculating the area of the polygon, we will want to avoid the area of the top red triangle. But the same area at the bottom should be taken into account.
■ Similarly, in the case of line segment BC, the top green triangle should be avoided while taking the area of the polygon. But the bottom green triangle should be taken into account. Note that the two green triangles are equal.
■ There is a pair of equal triangles at each line segment of the polygon. One more example: In the case of line segment EF, the top grey triangle should be avoided while taking the area of the polygon. But the bottom grey triangle should be taken into account. Note that the two grey triangles are equal.
■ So we can conclude that, the area of the histogram and polygon are equal
Draw a frequency polygon corresponding to this frequency distribution table.
Solution:
First we draw the histogram. But in the histogram, we find that there is no space between the zero and the beginning of the first class-interval. In such cases we adopt the following procedure:
1. We extend the x-axis towards the left. That is., in the negative direction. This is shown in the fig.25.18 below.
2. Now there is enough space. We can provide an imaginary class-interval in this space.
The lower limit of this new class-interval = 0- class width = 0 – 10 = -10.
So the new imaginary class-interval is [(-10)-0]
3. The midpoint A' of this class-interval will be at (-5,0)
4. Join A' to B. The segment A'B will cut the y-axis at A
5. For convenience we will name the origin zer as 'O'.
6. So the required polygon is OABCDEFGHIJKL. Thus we can complete the polygon.
Let us see how this can be done:
• We drew the polygon by connecting the midpoints. These midpoints can be calculated from the data table itself. There is no need of a histogram to find the midpoints
• So, we need the midpoints. That is., the exact middle of each class-intervals. The midpoints of the class-intervals are called class-marks.
• The class-mark of any class-interval is given by:
• Having the midpoints is not good enough. We want the 'heights' also. The 'heights', which are the y coordinates, are obviously the frequencies. There are no calculations involving them.
Let us see an example:
In a city, the weekly observations made in a study on the 'cost of living index' are given in the following table:
Draw a frequency polygon for the data above (without constructing a histogram).
Solution:
1. We want to draw the frequency polygon without drawing the histogram. So we need to find the midpoints from the data table. That means, we need to find the class-marks
• Class mark of the first interval = (140+150)/2 = 290/2 = 145
• Class mark of the second interval = (150+160)/2 = 310/2 = 155
In this way, the class marks of all the intervals are calculated and is shown in the table below
2. Using this table, we can draw the frequency polygon. It is shown in the fig.25.19 below:
• Note that, a class-interval of 130-140 (with frequency zero) is assumed at the beginning.
• Also a class-interval of 200-210 (with frequency zero) is assumed at the end.
• The midpoints of these two classes are marked as A and H. Then only we can complete the polygon.
A sample point:
• Consider the vertex E of the polygon. It corresponds to the class-interval 170-180. So actually, it corresponds to the class-mark 175. Thus, the x coordinate of E is 175.
• Now, the y-coordinate of E is the frequency corresponding to the class-interval 170-180, which is 9. Thus, the coordinates of E are (175,9)
We can see that:
• the x position of E lies in the midway between 170 and 180
• the y position of E lies midway between the horizontal lines through 8 and 10
• If we draw it on a graph paper, the thin subdivision lines will help us to mark the points accurately.
Now we will see some solved examples:
Solved example 25.17
The following table gives the distribution of students of two sections according to the marks obtained by them:
Represent the marks of the students of both the sections on the same graph by two frequency polygons.
Solution:
1. We want to draw the frequency polygon without drawing the histogram. So we need to find the midpoints from the data table. That means, we need to find the class-marks
• Class mark of the first interval = (0+10)/2 = 10/2 = 5
• Class mark of the second interval = (10+20)/2 = 30/2 = 15
In this way, the class marks of all the intervals are calculated and is shown in the table below
2. Using this table, we can draw the frequency polygons. They are shown in the fig.25.20 below:
• Note that, a class-interval of [(-10)-0] (with frequency zero) is assumed at the beginning.
• Also a class-interval of 50-60 (with frequency zero) is assumed at the end.
• The blue polygon OABCDEFG is for Section A and the green polygon OPQRSTUV is for Section B
• While drawing on graph paper different coloured pens or pencils may be used so that, they can be distinguished from each other
• If different colours are not available, one polygon may be drawn with solid lines, while the other with dashed lines
A sample point:
• Consider the vertex F of the blue polygon. It corresponds to the class-interval 40-50. So actually, it corresponds to the class-mark 45. Thus, the x coordinate of F is 45.
• Now, the y-coordinate of F is the frequency corresponding to the class-interval 40-50, which is 9. Thus, the coordinates of E are (45,9)
We can see that:
• the x position of F lies in the midway between 40 and 50
• the y position of F lies midway between the horizontal lines through 8 and 10
• If we draw it on a graph paper, the thin subdivision lines will help us to mark the points accurately.
Based on the above example, let us discuss the advantage of frequency polygons:
• A teacher takes maths classes in STD IX A and IX B. She tabulated the marks obtained by the students in a test. One table for class A and another table for class B. Based on the tables she prepared histograms. One histogram for class A and another for class B
• So she finally has two histograms. With them, she can assess the performance of the students. Some of the information that can be obtained are:
♦ Whether a large number of students are getting below average marks
♦ Whether only a very few students are getting high marks
• She can get the above information separately for the two classes, from the two separate histograms.
■ But if she want to compare between the two classes, it would be difficult with the two separate histograms. In such a situation, frequency polygons are more suitable.
• In such cases, the two frequency polygons are drawn on the same graph paper. If the frequency polygon of a class is so large that it completely covers the other, then that class is certainly doing better.
Solved example 25.18
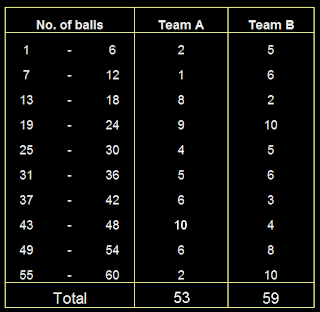
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:
Represent the data of both the teams on the same graph by frequency polygons. [Hint : First make the class intervals continuous.]
Solution:
1. If we use the above table to make the frequency polygon, there will be gaps between class intervals. So we have to make the class intervals continuous. The modified table is given below (see solved example 25.13) :
2. We want to draw the frequency polygon without drawing the histogram. So we need to find the midpoints from the data table. That means, we need to find the class-marks
• Class mark of the first interval = (0.5+6.5)/2 = 7/2 = 3.5
• Class mark of the second interval = (6.5+12.5)/2 = 19/2 = 9.5
In this way, the class marks of all the intervals are calculated and is shown in the table below:
3. Using this table, we can draw the frequency polygons. They are shown in the fig.25.21 below:
• Note that, a class-interval of [(-5.5)-0.5] (with frequency zero) is assumed at the beginning. (It's lower limit '-5.5' is obtained by subtracting the class width 6 from 0.5)
• Also a class-interval of 60.5-66.5 (with frequency zero) is assumed at the end.
• The blue polygon OABCDEFGHIJKL is for Team A and the green polygon OPQRSTUVWXYZN is for Team B
• While drawing on graph paper different coloured pens or pencils may be used so that, they can be distinguished from each other
• If different colours are not available, one polygon may be drawn with solid lines, while the other with dashed lines
A sample point:
• Consider the vertex U of the green polygon. It corresponds to the class-interval 24.5-30.5. So actually, it corresponds to the class-mark 27.5. Thus, the x coordinate of U is 27.7.
• Now, the y-coordinate of U is the frequency corresponding to the class-interval 24.5-30.5, which is 5. Thus, the coordinates of E are (27.5,5)
We can see that:
• the x position of U lies in the midway between 24.5 and 30.5
• the y position of U lies midway between the horizontal lines through 4 and 6
• If we draw it on a graph paper, the thin subdivision lines will help us to mark the points accurately.
Frequency polygon
We have learned about Bar graph and Histogram. Frequency polygon is the third method (for the pictorial representation of data) which we have to study in this chapter. Let us see it's details:Let us revisit the first histogram that we saw in this chapter. It is given in fig.25.6. To this histogram, do the following modifications:
1. Mark the midpoints of the upper edges of all the rectangles
2. Name these midpoints as B, C, D, E, F and G
3. Join these midpoints by line segments
These line segments are shown in blue colour in the fig.25.15 below:
We have not obtained the polygon yet. For that we continue the modification steps
4. Assume that there is a class interval before 30.5-35.5
What will be the limits of such an interval?
Ans: We know that the width is 5
• So the lower limit of that interval will be 30.5-5 = 25.5
• Thus the lower limit is 25.5, and upper limit is 30.5
5. Assume that there is a class interval after before 55.5-60.5
What will be the limits of such an interval?
Ans: We know that the width is 5
• So the upper limit of that interval will be 60.5+5 = 65.5
• Thus the lower limit is 60.5, and upper limit is 65.5
6. Mark the midpoint of 25.5-30.5 as A
Mark the midpoint of 60.5-65.5 as H
7. Draw the line segments AB and GH. This is shown in fig. 25.16 below:
 |
| Fig.25.16 |
Let us prove it:
1. In the fig.25.17 below, the line segment AB gives us two triangles. One at the top, and other at the bottom. They are shown in red colour.
 |
| Fig.25.17 |
3. The two triangles are enlarged and shown at the side of the fig.25.17. The top triangle is named as PBR, and the bottom triangle is named as AQR
(i) Line PQ is the left edge of the first rectangle in the histogram.
(ii) AQ lies on the x-axis
(iii) PB lies on the top edge of the first rectangle of the histogram
From the above three points it is clear that:
• PQ is perpendicular to PB. So ∠P = 90o. It is shown in white colour in the top triangle
• PQ is perpendicular to AQ. So ∠Q = 90o. It is shown in white colour in the bottom triangle
4. PB and AQ are parallel. They are cut by a transversal AB. So ∠B = ∠A. They are shown in yellow colour
5. ∠R is same in both triangles because, they are opposite angles. They are shown in blue colour
6. Length of AQ = half of class-interval 25.5-30.5 = half of 5 = 2.5
Length of PB = half of class-interval 30.5-35.5 = half of 5 = 2.5
Thus we get AQ = PB
7. So we have the following situation:
• In the upper triangle, there is a length PB of 2.5 cm, with white and yellow angles at it's ends
• In the bottom triangle, there is a length AQ of 2.5 cm, with white and yellow angles at it's ends
• It is a case of ASA congruence. The two red triangles AQR and BPR are equal.
Now we consider the area of histogram and the polygon. Note that:
• The top red triangle is inside the histogram. But it is outside the polygon• The bottom red triangle is outside the histogram but it is inside the polygon
■ So, while calculating the area of the polygon, we will want to avoid the area of the top red triangle. But the same area at the bottom should be taken into account.
■ Similarly, in the case of line segment BC, the top green triangle should be avoided while taking the area of the polygon. But the bottom green triangle should be taken into account. Note that the two green triangles are equal.
■ There is a pair of equal triangles at each line segment of the polygon. One more example: In the case of line segment EF, the top grey triangle should be avoided while taking the area of the polygon. But the bottom grey triangle should be taken into account. Note that the two grey triangles are equal.
■ So we can conclude that, the area of the histogram and polygon are equal
In the above example, the first class-interval begins from 30.5. So there is plenty of space between zero and the beginning of the histogram. We can utilise this space to provide a new class-interval at the beginning so that the polygon can be completed.
What if the original first class-interval begins at zero itself? Let us see such an example:
Consider the marks, out of 100, obtained by 51 students of a class in a test:
Solution:
First we draw the histogram. But in the histogram, we find that there is no space between the zero and the beginning of the first class-interval. In such cases we adopt the following procedure:
1. We extend the x-axis towards the left. That is., in the negative direction. This is shown in the fig.25.18 below.
 |
| Fig.25.18 |
The lower limit of this new class-interval = 0- class width = 0 – 10 = -10.
So the new imaginary class-interval is [(-10)-0]
3. The midpoint A' of this class-interval will be at (-5,0)
4. Join A' to B. The segment A'B will cut the y-axis at A
5. For convenience we will name the origin zer as 'O'.
6. So the required polygon is OABCDEFGHIJKL. Thus we can complete the polygon.
From the above examples, we get a new idea:
■ We can draw a frequency polygon without the help of a histogram. Let us see how this can be done:
• We drew the polygon by connecting the midpoints. These midpoints can be calculated from the data table itself. There is no need of a histogram to find the midpoints
• So, we need the midpoints. That is., the exact middle of each class-intervals. The midpoints of the class-intervals are called class-marks.
• The class-mark of any class-interval is given by:
Let us see an example:
In a city, the weekly observations made in a study on the 'cost of living index' are given in the following table:
Solution:
1. We want to draw the frequency polygon without drawing the histogram. So we need to find the midpoints from the data table. That means, we need to find the class-marks
• Class mark of the first interval = (140+150)/2 = 290/2 = 145
• Class mark of the second interval = (150+160)/2 = 310/2 = 155
In this way, the class marks of all the intervals are calculated and is shown in the table below
 |
| Fig.25.19 |
• Also a class-interval of 200-210 (with frequency zero) is assumed at the end.
• The midpoints of these two classes are marked as A and H. Then only we can complete the polygon.
A sample point:
• Consider the vertex E of the polygon. It corresponds to the class-interval 170-180. So actually, it corresponds to the class-mark 175. Thus, the x coordinate of E is 175.
• Now, the y-coordinate of E is the frequency corresponding to the class-interval 170-180, which is 9. Thus, the coordinates of E are (175,9)
We can see that:
• the x position of E lies in the midway between 170 and 180
• the y position of E lies midway between the horizontal lines through 8 and 10
• If we draw it on a graph paper, the thin subdivision lines will help us to mark the points accurately.
Solved example 25.17
The following table gives the distribution of students of two sections according to the marks obtained by them:
Solution:
1. We want to draw the frequency polygon without drawing the histogram. So we need to find the midpoints from the data table. That means, we need to find the class-marks
• Class mark of the first interval = (0+10)/2 = 10/2 = 5
• Class mark of the second interval = (10+20)/2 = 30/2 = 15
In this way, the class marks of all the intervals are calculated and is shown in the table below
 |
| Fig.25.20 |
• Also a class-interval of 50-60 (with frequency zero) is assumed at the end.
• The blue polygon OABCDEFG is for Section A and the green polygon OPQRSTUV is for Section B
• While drawing on graph paper different coloured pens or pencils may be used so that, they can be distinguished from each other
• If different colours are not available, one polygon may be drawn with solid lines, while the other with dashed lines
A sample point:
• Consider the vertex F of the blue polygon. It corresponds to the class-interval 40-50. So actually, it corresponds to the class-mark 45. Thus, the x coordinate of F is 45.
• Now, the y-coordinate of F is the frequency corresponding to the class-interval 40-50, which is 9. Thus, the coordinates of E are (45,9)
We can see that:
• the x position of F lies in the midway between 40 and 50
• the y position of F lies midway between the horizontal lines through 8 and 10
• If we draw it on a graph paper, the thin subdivision lines will help us to mark the points accurately.
• A teacher takes maths classes in STD IX A and IX B. She tabulated the marks obtained by the students in a test. One table for class A and another table for class B. Based on the tables she prepared histograms. One histogram for class A and another for class B
• So she finally has two histograms. With them, she can assess the performance of the students. Some of the information that can be obtained are:
♦ Whether a large number of students are getting below average marks
♦ Whether only a very few students are getting high marks
• She can get the above information separately for the two classes, from the two separate histograms.
■ But if she want to compare between the two classes, it would be difficult with the two separate histograms. In such a situation, frequency polygons are more suitable.
• In such cases, the two frequency polygons are drawn on the same graph paper. If the frequency polygon of a class is so large that it completely covers the other, then that class is certainly doing better.
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:
Solution:
1. If we use the above table to make the frequency polygon, there will be gaps between class intervals. So we have to make the class intervals continuous. The modified table is given below (see solved example 25.13) :
• Class mark of the first interval = (0.5+6.5)/2 = 7/2 = 3.5
• Class mark of the second interval = (6.5+12.5)/2 = 19/2 = 9.5
In this way, the class marks of all the intervals are calculated and is shown in the table below:
 |
| Fig.25.21 |
• Also a class-interval of 60.5-66.5 (with frequency zero) is assumed at the end.
• The blue polygon OABCDEFGHIJKL is for Team A and the green polygon OPQRSTUVWXYZN is for Team B
• While drawing on graph paper different coloured pens or pencils may be used so that, they can be distinguished from each other
• If different colours are not available, one polygon may be drawn with solid lines, while the other with dashed lines
A sample point:
• Consider the vertex U of the green polygon. It corresponds to the class-interval 24.5-30.5. So actually, it corresponds to the class-mark 27.5. Thus, the x coordinate of U is 27.7.
• Now, the y-coordinate of U is the frequency corresponding to the class-interval 24.5-30.5, which is 5. Thus, the coordinates of E are (27.5,5)
We can see that:
• the x position of U lies in the midway between 24.5 and 30.5
• the y position of U lies midway between the horizontal lines through 4 and 6
• If we draw it on a graph paper, the thin subdivision lines will help us to mark the points accurately.
In the next section we will see measures of central tendency.
Thank you, you have cleared my confusion.
ReplyDeleteThank you, my confusion is now solved.
ReplyDeleteThanks a lot
ReplyDeleteThanks a lot
ReplyDelete