In the previous section we saw how to use the height of a square pyramid to calculate it's lateral surface area. We also saw some solved examples. In this section, we will see volume of a square pyramid.
We know how to calculate the volume of prisms. Simply multiply the base area of the prism with it's height. To find the volume of a square pyramid, we will do an experiment:
1. Make a square pyramid using thick paper. See fig.33.16(a) below:
2. Make a square prism having the same height and same base area. (fig.33.16.b)
• At this stage, both the pyramid and prism are empty. This is shown in fig.33.17(a) below:
3. Fill the pyramid completely with sand
• Now the pyramid is full with sand. But the prism is empty. This is shown in fig.33.17(b)
4. Transfer this sand into the prism.
• Now the pyramid is empty. But the prism contains some sand. This is shown in fig.33.17(c)
• Some thing is not right. The pyramid was completely full. All the sand was transferred. But the prism is only partially full
• But this is natural. It happens because the volume of a square pyramid will be less than the volume of a square prism having same base area and same height.
• Let us try to find out how much the pyramid is smaller
5. Measure the height of the sand in the prism. We will see that it is one third of the total height of the prism. This is shown in fig.c
6. Now let us calculate the volumes:
(i) Let Vs be the volume of sand. From fig.c, we will get: Vs = base area × height = a2 × h⁄3.
(ii) Let Vpr be the volume of the prism. Obviously, Vpr = base area × height = a2 × h.
7. Taking ratios, we get:
• This is same as: Vs = 1⁄3 × Vpr
8. So volume of the sand is only one third of the volume of the prism
• But volume of the sand is same as the volume of the pyramid. So we can write:
• Volume of the square pyramid = 1⁄3 × Vpr = 1⁄3 × (a2h)
♦ Where a is the base edge of the square pyramid
♦ And h is the height of the square pyramid
• We will see the actual derivation of this formula in higher classes
An example:
Find the volume of a square pyramid of base edge 10 cm and height 8 cm
Solution:
1. Given: a = 10 cm, h = 8 cm
2. Then volume = 1⁄3 × (a2h) = 1⁄3 × 102 × 8 = 2662⁄3 cm3
Another example:
A metal cube of side 15 cm is melted and recast into a square pyramid of base edge 25 cm. What is it's height?
Solution:
1. Volume of the given cube = 153 cm3
2. Volume of the square pyramid will also be 153 cm3
3. So we can write: 1⁄3 × (a2h) = 1⁄3 × 252 × h = 153
⟹ h = 3 × 152⁄253 = 16.2 cm
Now we will see some solved examples
Solved example 33.10
What is the volume of a square pyramid of base edge 10 cm and slant height 15 cm
Solution:
In this problem, we are not given h. But h is essential to calculate volume. So we will find it first.
1. Imagine the ⊿OAB inside the pyramid. See fig.33.18(a) below:
• It should satisfy the following conditions:
♦ OAB must be right angled
♦ O must coincide with the centre of the base
♦ A must coincide with the midpoint of a base edge
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid
♦ OA = half of base edge = 5 cm
♦ AB = slant height = 15 cm
2. Applying Pythagoras theorem, we get:
h = OB = √[152 - 52] = √[225 - 25] = √[200] = 10√2 cm
3. Then volume = 1⁄3 × (a2h) = 1⁄3 × 102 × 10√2 = 1⁄3 × (1000√2) cm3
Solved example 33.11
Two square pyramids have the same volume. The base edge of one is half that of the other. How many times the height of the second pyramid is the height of the first?
Solution:
1. Let the volume, base edge and height of the first pyramid be V1, a1 and h1 respectively
• Let the volume, base edge and height of the second pyramid be V2, a2 and h2 respectively
2. Then volume of first pyramid = V1 = 1⁄3 × [(a1)2h1]
• Volume of second pyramid = V2 = 1⁄3 × [(a2)2h2]
3. Given that V1 = V2
• So we can write: 1⁄3 × [(a1)2h1)] = 1⁄3 × [(a2)2h2]
⟹ [(a1)2h1] = [(a2)2h2]
4. But given that a2 = a1⁄2
• Substituting this in (3), we get: [(a1)2h1] = [(a1⁄2)2h2]
⟹ [(a1)2h1] = 1⁄4 × [(a1)2h2] ⟹ [h1] = 1⁄4 × [h2] ⟹ 4[h1] = [h2]
• So height of the second pyramid (whose base edge is half) is four times the height of the first pyramid
Solved example 33.12
The base edge of two square pyramids are in the ratio 1:2 and their heights are in the ratio 1:3. The volume of the first is 180 cm3. What is the volume of the second?
Solution:
1. Let the volume, base edge and height of the first pyramid be V1, a1 and h1 respectively
• Let the volume, base edge and height of the second pyramid be V2, a2 and h2 respectively
2. (i) Then volume of first pyramid = V1 = 1⁄3 × [(a1)2h1]
(ii) Volume of second pyramid = V2 = 1⁄3 × [(a2)2h2]
3. Given that a1⁄a2 = 1⁄2 . So we get: a1 = a2⁄2
4. Given that h1⁄h2 = 1⁄3 . So we get: h1 = h2⁄3
5. Substituting (3) and (4) in 2(i), we get:
• V1 = 180 = 1⁄3 × [(a2⁄2)2 × h2⁄3] ⟹ 180 × 3 = [(a2⁄2)2 × h2⁄3] ⟹ 540 = 1⁄4 × 1⁄3 × [(a2)2h2]
⟹ 540 × 4 = 1⁄3 × [(a2)2h2]
• So we get the value of 1⁄3 × [(a2)2h2]. But this is V2
• Thus, the volume of the second pyramid = V2 = 540 × 4 = 2160 cm3.
Solved example 33.13
All edges of a square pyramid are 18 cm. What is it's volume?
Solution:
In this problem, we are not given h. But h is essential to calculate volume. So we will find it first.
1. Imagine ⊿OCB inside the pyramid. See fig.33.18.b above
• It should satisfy the following conditions:
♦ OCB must be right angled
♦ O must coincide with the centre of the base
♦ C must coincide with a corner the base square
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid
♦ OC = half of a diagonal of the base
♦ BC = Lateral edge = 18 cm
2. Applying Pythagoras theorem, we get:
OB = √[BC2 - OC2] = √[182 - OC2]
3. Now OC = half of the diagonal
• Full diagonal = √[182 + 182] = 18√2 cm. See fig.33.18.c
• So half diagonal = OC = 9√2
4. Substituting this value of OC in (2), we get:
• OB = √[182 - (9√2)2] = √[324-(81×2)] = √[162] cm
5. Then volume = 1⁄3 × (a2h) = 1⁄3 × 182 × √162 = 1⁄3 × 182 × √[9×9×2] = 972√2 cm3 .
Solved example 33.14
The slant height of a square pyramid is 25 cm and it's surface area is 896 cm2. What is it's volume?
Solution:
1. Let the base edge be (2a) cm
2. Then area of one isosceles triangle = 1⁄2 × base × altitude = 1⁄2 × (2a) × 25 = 25a cm2.
• Area of four isosceles triangles = 4×25a = 100a cm2.
3. Base area = (2a)2 = 4a2 cm2.
4. Total surface area = (100a + 4a2) cm2
5. But the total surface area is given as 896 cm2. So we can write: (100a + 4a2) = 896
6. Dividing both sides by 4 we get: (25a + a2) = 224
⟹ a2 + 25a - 224 = 0
7. To avoid any confusion, we will use 'x' instead of 'a'. Then we get:
x2 + 25x - 224 = 0
8. This is a quadratic equation of the form ax2 + bx + c = 0 (Details here)
In the next section, we will see cones.
We know how to calculate the volume of prisms. Simply multiply the base area of the prism with it's height. To find the volume of a square pyramid, we will do an experiment:
1. Make a square pyramid using thick paper. See fig.33.16(a) below:
 |
| Fig.33.16 |
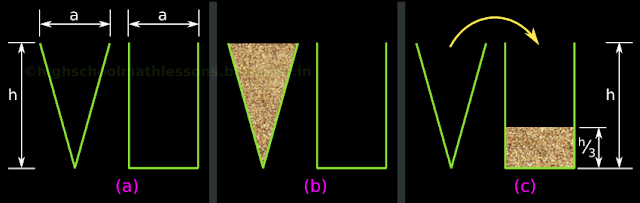
• At this stage, both the pyramid and prism are empty. This is shown in fig.33.17(a) below:
 |
| Fig.33.17 |
• Now the pyramid is full with sand. But the prism is empty. This is shown in fig.33.17(b)
4. Transfer this sand into the prism.
• Now the pyramid is empty. But the prism contains some sand. This is shown in fig.33.17(c)
• Some thing is not right. The pyramid was completely full. All the sand was transferred. But the prism is only partially full
• But this is natural. It happens because the volume of a square pyramid will be less than the volume of a square prism having same base area and same height.
• Let us try to find out how much the pyramid is smaller
5. Measure the height of the sand in the prism. We will see that it is one third of the total height of the prism. This is shown in fig.c
6. Now let us calculate the volumes:
(i) Let Vs be the volume of sand. From fig.c, we will get: Vs = base area × height = a2 × h⁄3.
(ii) Let Vpr be the volume of the prism. Obviously, Vpr = base area × height = a2 × h.
7. Taking ratios, we get:
• This is same as: Vs = 1⁄3 × Vpr
8. So volume of the sand is only one third of the volume of the prism
• But volume of the sand is same as the volume of the pyramid. So we can write:
• Volume of the square pyramid = 1⁄3 × Vpr = 1⁄3 × (a2h)
♦ Where a is the base edge of the square pyramid
♦ And h is the height of the square pyramid
• We will see the actual derivation of this formula in higher classes
An example:
Find the volume of a square pyramid of base edge 10 cm and height 8 cm
Solution:
1. Given: a = 10 cm, h = 8 cm
2. Then volume = 1⁄3 × (a2h) = 1⁄3 × 102 × 8 = 2662⁄3 cm3
Another example:
A metal cube of side 15 cm is melted and recast into a square pyramid of base edge 25 cm. What is it's height?
Solution:
1. Volume of the given cube = 153 cm3
2. Volume of the square pyramid will also be 153 cm3
3. So we can write: 1⁄3 × (a2h) = 1⁄3 × 252 × h = 153
⟹ h = 3 × 152⁄253 = 16.2 cm
Now we will see some solved examples
Solved example 33.10
What is the volume of a square pyramid of base edge 10 cm and slant height 15 cm
Solution:
In this problem, we are not given h. But h is essential to calculate volume. So we will find it first.
1. Imagine the ⊿OAB inside the pyramid. See fig.33.18(a) below:
 |
| Fig.33.18 |
♦ OAB must be right angled
♦ O must coincide with the centre of the base
♦ A must coincide with the midpoint of a base edge
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid
♦ OA = half of base edge = 5 cm
♦ AB = slant height = 15 cm
2. Applying Pythagoras theorem, we get:
h = OB = √[152 - 52] = √[225 - 25] = √[200] = 10√2 cm
3. Then volume = 1⁄3 × (a2h) = 1⁄3 × 102 × 10√2 = 1⁄3 × (1000√2) cm3
Solved example 33.11
Two square pyramids have the same volume. The base edge of one is half that of the other. How many times the height of the second pyramid is the height of the first?
Solution:
1. Let the volume, base edge and height of the first pyramid be V1, a1 and h1 respectively
• Let the volume, base edge and height of the second pyramid be V2, a2 and h2 respectively
2. Then volume of first pyramid = V1 = 1⁄3 × [(a1)2h1]
• Volume of second pyramid = V2 = 1⁄3 × [(a2)2h2]
3. Given that V1 = V2
• So we can write: 1⁄3 × [(a1)2h1)] = 1⁄3 × [(a2)2h2]
⟹ [(a1)2h1] = [(a2)2h2]
4. But given that a2 = a1⁄2
• Substituting this in (3), we get: [(a1)2h1] = [(a1⁄2)2h2]
⟹ [(a1)2h1] = 1⁄4 × [(a1)2h2] ⟹ [h1] = 1⁄4 × [h2] ⟹ 4[h1] = [h2]
• So height of the second pyramid (whose base edge is half) is four times the height of the first pyramid
Solved example 33.12
The base edge of two square pyramids are in the ratio 1:2 and their heights are in the ratio 1:3. The volume of the first is 180 cm3. What is the volume of the second?
Solution:
1. Let the volume, base edge and height of the first pyramid be V1, a1 and h1 respectively
• Let the volume, base edge and height of the second pyramid be V2, a2 and h2 respectively
2. (i) Then volume of first pyramid = V1 = 1⁄3 × [(a1)2h1]
(ii) Volume of second pyramid = V2 = 1⁄3 × [(a2)2h2]
3. Given that a1⁄a2 = 1⁄2 . So we get: a1 = a2⁄2
4. Given that h1⁄h2 = 1⁄3 . So we get: h1 = h2⁄3
5. Substituting (3) and (4) in 2(i), we get:
• V1 = 180 = 1⁄3 × [(a2⁄2)2 × h2⁄3] ⟹ 180 × 3 = [(a2⁄2)2 × h2⁄3] ⟹ 540 = 1⁄4 × 1⁄3 × [(a2)2h2]
⟹ 540 × 4 = 1⁄3 × [(a2)2h2]
• So we get the value of 1⁄3 × [(a2)2h2]. But this is V2
• Thus, the volume of the second pyramid = V2 = 540 × 4 = 2160 cm3.
Solved example 33.13
All edges of a square pyramid are 18 cm. What is it's volume?
Solution:
In this problem, we are not given h. But h is essential to calculate volume. So we will find it first.
1. Imagine ⊿OCB inside the pyramid. See fig.33.18.b above
• It should satisfy the following conditions:
♦ OCB must be right angled
♦ O must coincide with the centre of the base
♦ C must coincide with a corner the base square
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid
♦ OC = half of a diagonal of the base
♦ BC = Lateral edge = 18 cm
2. Applying Pythagoras theorem, we get:
OB = √[BC2 - OC2] = √[182 - OC2]
3. Now OC = half of the diagonal
• Full diagonal = √[182 + 182] = 18√2 cm. See fig.33.18.c
• So half diagonal = OC = 9√2
4. Substituting this value of OC in (2), we get:
• OB = √[182 - (9√2)2] = √[324-(81×2)] = √[162] cm
5. Then volume = 1⁄3 × (a2h) = 1⁄3 × 182 × √162 = 1⁄3 × 182 × √[9×9×2] = 972√2 cm3 .
Solved example 33.14
The slant height of a square pyramid is 25 cm and it's surface area is 896 cm2. What is it's volume?
Solution:
1. Let the base edge be (2a) cm
2. Then area of one isosceles triangle = 1⁄2 × base × altitude = 1⁄2 × (2a) × 25 = 25a cm2.
• Area of four isosceles triangles = 4×25a = 100a cm2.
3. Base area = (2a)2 = 4a2 cm2.
4. Total surface area = (100a + 4a2) cm2
5. But the total surface area is given as 896 cm2. So we can write: (100a + 4a2) = 896
6. Dividing both sides by 4 we get: (25a + a2) = 224
⟹ a2 + 25a - 224 = 0
7. To avoid any confusion, we will use 'x' instead of 'a'. Then we get:
x2 + 25x - 224 = 0
8. This is a quadratic equation of the form ax2 + bx + c = 0 (Details here)
Where: a = 1, b = 25 and c = (-224)
9. So we can use the general formula to solve the equation
10. b2-4ac = 252-4×1×(-224) = 625 + 896 = 1521
• So √[b2-4ac] = √1521 = ±39
• This '±' sign is already present in the numerator in the formula
• The numerator is: -b±√[b2-4ac] = -(25)±39 = -25+39 OR -25-39
⟹ numerator = 14 OR -64
• The denominator = 2a = 2×1 = 2
• Thus x = 14⁄2 OR -64⁄2 ⟹ x = 7 OR -32
♦ The base edge cannot be negative value. So we get x = 7
• That is., half the base edge = a = 7 cm
11. Now we have the base edge and slant height. We want the height h
Imagine the ⊿OAB inside the pyramid. See fig.33.19(a) below:
• It should satisfy the following conditions:
♦ OAB must be right angled
♦ O must coincide with the centre of the base
♦ A must coincide with the midpoint of a base edge
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid
♦ OA = half of base edge = 7 cm
♦ AB = slant height = 25 cm
12. Applying Pythagoras theorem, we get:
h = OB = √[252 - 72] = √[625 - 49] = √[576] = 24 cm
13. Then volume = 1⁄3 × [(2a)2h] = 1⁄3 × 142 × 24 = 1568 cm3 ('2a' is used because, in this problem, the base edge is taken as '2a')
Solved example 33.15
All edges of a square pyramid are of the same length and it's height is 12 cm. What is it's volume?
Solution:
1. Let all the edges of the square prism be 'a'. Then we will get fig.33.19(b) above. The sides of the square are 'a'. The lateral edge BC is also 'a'.
• The triangle OCB must satisfy the following conditions:
♦ OCB must be right angled
♦ O must coincide with the centre of the base
♦ C must coincide with a corner the base square
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid
♦ OC = half of a diagonal of the base
♦ BC = Lateral edge = a cm
2. Applying Pythagoras theorem, we get:
OB = √[BC2 - OC2] = √[a2 - OC2]
3. Now OC = half of the diagonal
• Full diagonal = √[a2 + a2] = a√2 cm. See fig.33.19.c
• So half diagonal = OC = 1⁄2 × a√2 = a⁄(√2).
4. Substituting this value of OC in (2), we get:
• OB = √[a2 - (a⁄(√2))2] = √[a2 - a2⁄2] = √[a2⁄2] = a⁄(√2) cm
• But OB is the height which is given as 12 cm. So we get:
a⁄(√2) = 12 ⟹ a = 12√2 cm
5. Then volume = 1⁄3 × (a2h) = 1⁄3 × (12√2)2 × 12 = (12√2)2 × 4 = 144×2×4 = 1152 cm3.
Solved example 33.16
What is the surface area of a square pyramid of base perimeter 64 cm and volume 1280 cm3 ?
Solution:
1. base perimeter is given as 64 cm. So base edge = 64⁄4 = 16 cm
2. Volume is given as 1280 cm3. So we can write:
1280 = 1⁄3 × (a2h) = 1⁄3 × 162 × h ⟹ 1280 × 3 = 162 × h ⟹ 3840 = 162 × h ⟹ h = 15 cm
3. Now we have to find the slant height
• Triangle OAB should satisfy the following conditions:
♦ OAB must be right angled
♦ O must coincide with the centre of the base
♦ A must coincide with the midpoint of a base edge
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid = 15 cm
♦ OA = half of base edge = 8 cm
♦ AB = slant height
4. Applying Pythagoras theorem, we get:
AB = √[152 + 82] = √[225 + 64] = √[289] = 17 cm
5. Then area of one isosceles triangle = 1⁄2 × base × altitude = 1⁄2 × 16 × 17 = 136 cm2.
• Area of four isosceles triangles = 4×136 = 544 cm2.
3. Base area = 162 = 256 cm2.
4. Total surface area = (544 + 256) = 800 cm2
• This '±' sign is already present in the numerator in the formula
• The numerator is: -b±√[b2-4ac] = -(25)±39 = -25+39 OR -25-39
⟹ numerator = 14 OR -64
• The denominator = 2a = 2×1 = 2
• Thus x = 14⁄2 OR -64⁄2 ⟹ x = 7 OR -32
♦ The base edge cannot be negative value. So we get x = 7
• That is., half the base edge = a = 7 cm
11. Now we have the base edge and slant height. We want the height h
Imagine the ⊿OAB inside the pyramid. See fig.33.19(a) below:
 |
| Fig.33.19 |
♦ OAB must be right angled
♦ O must coincide with the centre of the base
♦ A must coincide with the midpoint of a base edge
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid
♦ OA = half of base edge = 7 cm
♦ AB = slant height = 25 cm
12. Applying Pythagoras theorem, we get:
h = OB = √[252 - 72] = √[625 - 49] = √[576] = 24 cm
13. Then volume = 1⁄3 × [(2a)2h] = 1⁄3 × 142 × 24 = 1568 cm3 ('2a' is used because, in this problem, the base edge is taken as '2a')
Solved example 33.15
All edges of a square pyramid are of the same length and it's height is 12 cm. What is it's volume?
Solution:
1. Let all the edges of the square prism be 'a'. Then we will get fig.33.19(b) above. The sides of the square are 'a'. The lateral edge BC is also 'a'.
• The triangle OCB must satisfy the following conditions:
♦ OCB must be right angled
♦ O must coincide with the centre of the base
♦ C must coincide with a corner the base square
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid
♦ OC = half of a diagonal of the base
♦ BC = Lateral edge = a cm
2. Applying Pythagoras theorem, we get:
OB = √[BC2 - OC2] = √[a2 - OC2]
3. Now OC = half of the diagonal
• Full diagonal = √[a2 + a2] = a√2 cm. See fig.33.19.c
• So half diagonal = OC = 1⁄2 × a√2 = a⁄(√2).
4. Substituting this value of OC in (2), we get:
• OB = √[a2 - (a⁄(√2))2] = √[a2 - a2⁄2] = √[a2⁄2] = a⁄(√2) cm
• But OB is the height which is given as 12 cm. So we get:
a⁄(√2) = 12 ⟹ a = 12√2 cm
5. Then volume = 1⁄3 × (a2h) = 1⁄3 × (12√2)2 × 12 = (12√2)2 × 4 = 144×2×4 = 1152 cm3.
Solved example 33.16
What is the surface area of a square pyramid of base perimeter 64 cm and volume 1280 cm3 ?
Solution:
1. base perimeter is given as 64 cm. So base edge = 64⁄4 = 16 cm
2. Volume is given as 1280 cm3. So we can write:
1280 = 1⁄3 × (a2h) = 1⁄3 × 162 × h ⟹ 1280 × 3 = 162 × h ⟹ 3840 = 162 × h ⟹ h = 15 cm
3. Now we have to find the slant height
• Triangle OAB should satisfy the following conditions:
♦ OAB must be right angled
♦ O must coincide with the centre of the base
♦ A must coincide with the midpoint of a base edge
♦ B must coincide with the apex
• We will get:
♦ OB = height of pyramid = 15 cm
♦ OA = half of base edge = 8 cm
♦ AB = slant height
4. Applying Pythagoras theorem, we get:
AB = √[152 + 82] = √[225 + 64] = √[289] = 17 cm
5. Then area of one isosceles triangle = 1⁄2 × base × altitude = 1⁄2 × 16 × 17 = 136 cm2.
• Area of four isosceles triangles = 4×136 = 544 cm2.
3. Base area = 162 = 256 cm2.
4. Total surface area = (544 + 256) = 800 cm2

Super
ReplyDelete