In the previous section we saw the slopes of perpendicular lines. We also saw some examples. In this section we will see circles.
• We have seen that y = mx + c is the equation of a line. What does it mean?
Let us analyze:
1. Consider a line whose equation is y = mx + c
2. Take any point 'P' on the line
• In the place of 'x' in the equation, put the x coordinate of the point
• In the place of 'y' in the equation, put the y coordinate of the point
3. Then the two sides of the equation will become equal. That is:
■ The coordinates of any point on the line will satisfy the equation of that line.
We can write the converse also:
■ If the coordinates of a point satisfy the equation of a line, then that point will lie on that line
Now consider a circle. Can we form a equation for that circle?
Let us try:
• There will be a large number of points in the circumference of a circle
♦ The coordinates of all those points should satisfy the equation of that circle
Let us see an example:
1. Consider the yellow circle in fig.34.29 below:
• It's center is at C(1,4). It's radius is 2 units
2. Consider any point P(x,y) on the circle. Then, using the distance formula,
CP = √[(x2-x1)2 + (y2-y1)]2 = √[(x-1)2 + (y-4)2]
3. But this distance CP is the radius of the circle
So we can write:
√[(x-1)2 + (y-4)2] = r = 2
4. Squaring both sides, we get:
[(x-1)2 + (y-4)2] = 4
5. The above equation can be taken as the equation of the circle because, every point on the circle will satisfy it.
• This is because, it is simply the square of the distance between the 'center of the circle' and 'the point on the circle'.
• And the distance from the center will be the same for which ever point we take.
An example:
(i) The point with coordinates (1,2) lies on the circle. This is shown in the fig.
(ii) The distance between C and that point = √[(x2-x1)2 + (y2-y1)2]
= √[(1-1)2 + (2-4)2] = √[(0)2 + (-2)2] = √[4] = 2 units
(iii) So 'square of the distance PO' = PO2 = 22= 4
The general case:
1. To write the general case, we consider a circle whose center is at any point C(x1,y1), and radius 'r' units
2. Then square of the distance between the center and any point (x,y) on the circle is:
[(x-x1)2 + (y-y1)2]
• But this distance is the square of the radius which is r2
3. Equating the two, we get:
[(x-x1)2 + (y-y1)2] = r2
• This is the general form of the equation of a circle
• Note the pattern:
♦ x1, which is the x coordinate of the center is subtracted from x
♦ y1, which is the y coordinate of the center is subtracted from y
4. From this we get the general form of the equation of any circle whose center (x1,y1) is at the origin O
• All we need to do is, put x1 = 0 and y1 = 0 in (3)
• Then we get: [x2 + y2] = r2
• This is shown in fig.34.30 below:
From this fig., we can see that:
• The distance from the center of the circle to any point on the circle is indeed '√[x2 + y2]' if the center is at the origin
Now we will see some solved examples:
Solved example 34.16
Find the equation of the line joining (1,2) and (2,4). In this, find the sequence of y coordinates of those points with the consecutive natural numbers 3, 4, 5, . . . as the x coordinates
Solution:
1. Equation of the line joining (1,2) and (2,4):
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (4-2)⁄(2-1) = 2⁄1 = 2
• 'c' of the line = (y1-mx1) = [2 - (2 × 1)] = [2 - 2] = 0
• So equation of the line is
y = mx + c:
y = 2 × x + 0 ⟹ y = 2x
2. We know that the consecutive natural numbers form a sequence. That sequence is:
1, 2, 3, 4, 5, . . .
3. The terms of this sequence form the x coordinates of some points. We can write them as:
(1, _ ), (2, _ ), (3, _ ), (4, _ ), (5, _ ), . . .
4. The y coordinates in the above sequence are left blank. We have to find their values.
• It is given that those y coordinates form a sequence
5. It is easy to find the terms of that sequence. Because we have the equation of the line. It is: y = 2x
• From the equation it is clear that, what ever be the value of x, the value of y will be twice that x value.
• So we can fill up the blank spaces in (3). We get:
(1,2), (2,4), (3,6), (4,8), (5,10), . . .
• Note that, the two points given to us in the question are the first two terms of the sequence.
• The line and the actual positions of the points are shown in the fig.34.31 below:
Solved example 34.17
Find the equation of the line joining (-1,3) and (2,5). Prove that if (u,v) is a point on this line, so is (u+3, v+2)
Solution:
1. Equation of the line joining (-1,3) and (2,5)
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (5-3)⁄(2-(-1)) = 2⁄3
• 'c' of the line = (y1-mx1) = [3 - (2⁄3 × -1)] = [3 + 2⁄3] = 11⁄3
• So equation of the line is
y = mx + c:
y = 2⁄3 × x + 11⁄3
2. Given that, (u,v) is a point on the line. What does that mean?
• It simply means that, any point on the line can be taken as (u,v)
• For example, if we consider the point (-1,3), we can take u = -1 and v = 3
• If we consider the point (2,5), we can take u = 2 and v = 5
3. Now we have prove that (u+3, v+2) is also a point on the line.
• For example, we know that (-1,3) is a point on the line.
♦ Then (-1+3, 3+2) should also be a point on the line.
♦ That is., (2,5) should also be a point on the line
• Similarly, we know that (2,5) is a point on the line.
♦ Then (2+3, 5+2) should also be a point on the line.
♦ That is., (5,7) should also be a point on the line
• We have to prove it for the general case.
4. Consider the rough sketch in fig 34.32 below:
• A possible position of (u+3, v+2) is shown.
• The slope of the line joining (u,v) and (u+3, v+2) is
m = (y2-y1)⁄(x2-x1) = (v+2-v)⁄(u+3-u) = 2⁄3
• But this is same slope of the line through (-1,3), (2,5) and (u,v)
• Also, (u,v) is a common point. So (u+3, v+2) will lie in the same line
Solved example 34.18
Prove that for any number u, the point (u, 2u+3) is on the line joining (-1,1), (2,7).
Solution:
1. Consider the rough sketch in fig.34.33 below
• We can mark any point P' on the x axis.
• If we draw a vertical line through that point it will surely meet the given line at some point.
2. Let the marked point P' on the x axis have an x coordinate of 'u'
• Then the meeting point P will also have the x coordinate 'u'
3. The y coordinate of P is not known
■ We have to prove that the y coordinate at the meeting point is:
[(2 times the x coordinate) + 3].
• In other words,
We have to prove that the y coordinate at the meeting point is:
2u+3
4. The equation of a line will help us to find the x coordinate when y coordinate is known
• The equation of a line will also help us to find the y coordinate when the x coordinate is known
5. So let us find the equation of the line:
Equation of the line joining (-1,1) and (2,7)
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (7-1)⁄(2-(-1)) = 6⁄3 = 2
• 'c' of the line = (y1-mx1) = [1 - (2 × -1)] = [1 + 2] = 3
• So equation of the line is
y = mx + c:
y = 2x + 3
6. From the equation it is clear that, at any point, the y coordinate will be:
[(2 times the x coordinate at that point) + 3]
Hence proved
Solved example 34.19
The x coordinate of a point on the slanted line in fig.34.34(a) is 3
(i) What is it's y coordinate?
(ii) What is the slope of the line?
(iii) Write the equation of the line
Solution:
Part (i):
1. Drop a perpendicular from B on to the x axis. Let B' be the foot of the perpendicular. This is shown in fig.b
• So BB' will be the y coordinate of B
2. The ⊿ABB' is a 30o 60o triangle. We can find it's sides using trigonometric properties. (Details here)
• But for that, at least one side of the triangle should be known.
We have:
♦ Length OB' = 3 units
♦ Length OA = 1 unit (since x coordinate of A = 1)
♦ So AB' = 3 - 1 = 2 units
So now we have one side. We can apply the properties of a 30o 60o triangle
• tan 60 = opposite side⁄adjacent side = BB'⁄AB' = BB'⁄2 = √3
⟹ BB' = 2√3
Thus y coordinate of B = BB' = 2√3
Part (ii):
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (2√3-0)⁄(3-1) = (2√3)⁄(2) = √3
Another method:
• If we know the angle θ that a line makes with the horizontal, then the slope of that line is simply tanθ.
• We discussed about it earlier in this chapter. Details here.
• For our present case, slope = tan 60 = √3
Part (iii):
Equation of the line joining (1,0) and (3,2√3)
• Slope of the line = m = √3
• 'c' of the line = (y1-mx1) = [0 - (√3 × 1)] = [0 - √3] = -√3
• So equation of the line is
y = mx + c:
y = √3x - √3 ⟹ y = √3(x-1)
Solved example 34.20
In the fig.34.35(a), ABCD is a square.
Prove that for any point on the diagonal BD, the sum of x and y coordinates is zero
Solution:
1. The vertices A and C are diagonally opposite. If we are given two such points in a rectangle or a square, we can easily find the coordinates of the other two vertices. Details here.
• So the unknown coordinates at B and D are shown in fig.b
2. Now we have two points on the line BD. We can write the equation
• Equation of the line joining (2,-2) and (-2,2)
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (2-(-2))⁄(-2-2) = 4⁄-2 = -2
• 'c' of the line = (y1-mx1) = [-2 - (-2 × 2)] = [-2 + 4] = 2
• So equation of the line is
y = mx + c:
y = -2x + 2
Solved example 34.21
Prove that for any point on the line intersecting the axes in the fig.34.36 below, the sum of the x and y coordinates is 3
Solution:
1. We have the coordinates of two points on the line.
• Using them we can write the equation of the line
• Equation of the line joining (3,0) and (0,3)
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (3-0)⁄(0-3) = 3⁄-3 = -1
• 'c' of the line = (y1-mx1) = [0 - (-1 × 3)] = [0 - (-3)] = 3
• So equation of the line is
y = mx + c:
y = -1x + 3
2. From this equarion we get: x+y = 3
That is., for every point on this line, the sum of x and y coordinates will be 3
Solved example 34.22
Find the equation of the circle with center at the origin and radius 5 cm. Write the coordinates of 8 points on this circle
Solution:
1. We have seen at the beginning of this section that:
Equation of a circle with center O and radius r is
[x2 + y2] = r2.
• So for our present case, the equation is: [x2 + y2] = 52 ⟹ [x2 + y2] = 25
2. The circle cuts the axes at the following four points:
(i) P at the positive side of the x axis
(ii) P' at the negative side of the x axis
(iii) Q at the positive side of the y axis
(ii) Q' at the negative side of the y axis
These are shown in the fig.34.37(a) below:
• Now we will calculate the coordinates of each of the above four points
(i) Point P: Since the point P is on the x axis, the y coordinate will be equal to zero.
• So put y = 0 in the equation of the circle in (1)
• We get: [x2 + 0] = 25 ⟹ x2 = 25 ⟹ x = √25 = ±5
• There will be two roots for 25. They are +5 and -5.
• That means, the circle will intersect with the x axis at two points.
♦ One point is P on the positive side of the x axis. The coordinates are (5,0)
♦ The other point P' is on the negative side of the x axis. The coordinates are (-5,0)
• This is shown in the fig.30.37(a) above
• So we started out to find P and got both P and P'
(ii) Point P': This is already obtained above
(iii) Point Q: Since the point Q is on the y axis, the x coordinate will be equal to zero.
• So put x = 0 in the equation of the circle in (1)
• We get: [0 + y2] = 25 ⟹ y2 = 25 ⟹ y = √25 = ±5
• There will be two roots for 25. They are +5 and -5.
• That means, the circle will intersect with the y axis at two points.
♦ One point Q is on the positive side of the y axis. The coordinates are (0,5)
♦ The other point Q' is on the negative side of the y axis. The coordinates are (0,-5)
• This is shown in the fig.30.37(a) above
• So we started out to find Q and got both Q and Q'
(ii) Point Q': This is already obtained above
3. We want four more points.
• For that, we draw a line at an angle of 60o with the positive side of the x axis.
♦ This line meets the circle at R. This is shown in fig.34.37(b) above
• A perpendicular is dropped from R on to the x axis. The foot of the perpendicular is R'
♦ Now x coordinate of R will be equal to OR'
♦ y coordinate of R will be equal to RR'
• This is a problem similar to solved example 34.19 that we saw above. In that problem we used the trigonometrical ratio tan. In this example we will use sine and cosine
Consider ⊿ORR'. We have:
• sin 60 = opposite side⁄hypotenuse = RR'⁄OR = RR'⁄5
But from the tables, sin 60 = √3⁄2
So we can write: RR'⁄5 = √3⁄2 ⟹ RR' = (5√3)⁄2
• cos 60 = adjacent side ⁄hypotenuse = OR'⁄OR = OR'⁄5
But from the tables, cos 60 = 1⁄2
So we can write: OR'⁄5 = 1⁄2 ⟹ OR' = 5⁄2
Thus the coordinates of R are: [5⁄2 , (5√3)⁄2]
Check:
• Applying Pythagoras theorem in ⊿ORR', we have:
OR = √[(OR')2 + (RR')2] = √[(5⁄2)2 + ((5√3)⁄2)2] = √[25⁄4 + 75⁄4] = √[100⁄4] = √[25] = 5 units
• The radius is given as 5 cm. So our calculations are correct
4. Three more points can be obtained in the same way. They are: S, S'' and R''. They are shown in fig.b. They are symmetrical to the point R that we calculated above. So the coordinates can be written easily:
Point S: [-5⁄2 , (5√3)⁄2]
Point S'': [-5⁄2 , (-5√3)⁄2]
Point R'': [5⁄2 , (-5√3)⁄2]
Solved example 34.23
Let (x,y) be a point on the circle with the line joining (0,1) and (2,3) as diameter.
(i) Prove that x2+ y2 - 2x - 4y +3 = 0.
(ii) Find the coordinates of the points where the circle cuts the x axis
Solution:
1. The end points of a diameter are (0,1) and (2,3)
From this we get:
• x coordinate of the midpoint = (x1+x2)⁄2 = (0+2)⁄2 = 2⁄2 = 1
• y coordinate of the midpoint = (y1+y2)⁄2 = (1+3)⁄2 = 4⁄2 = 2
• So the coordinates of the midpoint are (Details here): (1,2)
• But the midpoint of the diameter is same as the center of the circle
2. Length of the diameter can be calculated using the distance formula:
Diameter = √[(x2-x1)2 + (y2-y1)]2 = √[(2-0)2 + (3-1)2] = √[(2)2 + (2)2] = √8 = √[2×4] = 2√2
• So radius = (2√2)⁄2 = √2 units
3. The general form of the equation of any circle whose center is at any point C(x1,y1), and radius is 'r' units is: [(x-x1)2 + (y-y1)2] = r2.
• So we get the equation of our circle:
[(x-1)2 + (y-2)2] = (√2)2.
• Expanding the above expression, we get:
x2 -2x + 1 + y2 - 4y + 4 = 2 ⟹ x2+ y2 - 2x - 4y +3 = 0
Part (ii):
1. At the points where the circle cuts the x axis, the y coordinates will be zero.
2. So we can put y = 0 in the equation of the circle:
x2+ 02 - 2x - 4×0 +3 = 0 ⟹ x2 - 2x +3 = 0
Solution:
• We know that, the axes are always perpendicular to each other
• In this problem, the point of intersection of the axes, that is., the origin, lies on the circle
• So AB will be a diameter of the circle (Details here)
1. The end points of a diameter are (0,2) and (4,0)
From this we get:
• x coordinate of the midpoint = (x1+x2)⁄2 = (0+4)⁄2 = 4⁄2 = 2
• y coordinate of the midpoint = (y1+y2)⁄2 = (2+0)⁄2 = 2⁄2 = 1
• So the coordinates of the midpoint are (Details here): (2,1)
• But the midpoint of the diameter is same as the center of the circle
2. Length of the diameter can be calculated using the distance formula:
Diameter = √[(x2-x1)2 + (y2-y1)]2 = √[(4-0)2 + (0-2)2] = √[(4)2 + (-2)2] = √20 = √[5×4] = 2√5
• So radius = (2√5)⁄2 = √5 units
3. The general form of the equation of any circle whose center is at any point C(x1,y1), and radius is 'r' units is: [(x-x1)2 + (y-y1)2] = r2.
• So we get the equation of our circle:
[(x-2)2 + (y-1)2] = (√5)2.
• Expanding the above expression, we get:
x2 -4x + 4 + y2 - 2y + 1 = 5 ⟹ x2+ y2 - 4x - 2y = 0
In the next section, we will see Polynomials.
• We have seen that y = mx + c is the equation of a line. What does it mean?
Let us analyze:
1. Consider a line whose equation is y = mx + c
2. Take any point 'P' on the line
• In the place of 'x' in the equation, put the x coordinate of the point
• In the place of 'y' in the equation, put the y coordinate of the point
3. Then the two sides of the equation will become equal. That is:
■ The coordinates of any point on the line will satisfy the equation of that line.
We can write the converse also:
■ If the coordinates of a point satisfy the equation of a line, then that point will lie on that line
Now consider a circle. Can we form a equation for that circle?
Let us try:
• There will be a large number of points in the circumference of a circle
♦ The coordinates of all those points should satisfy the equation of that circle
Let us see an example:
1. Consider the yellow circle in fig.34.29 below:
 |
| Fig.34.29 |
2. Consider any point P(x,y) on the circle. Then, using the distance formula,
CP = √[(x2-x1)2 + (y2-y1)]2 = √[(x-1)2 + (y-4)2]
3. But this distance CP is the radius of the circle
So we can write:
√[(x-1)2 + (y-4)2] = r = 2
4. Squaring both sides, we get:
[(x-1)2 + (y-4)2] = 4
5. The above equation can be taken as the equation of the circle because, every point on the circle will satisfy it.
• This is because, it is simply the square of the distance between the 'center of the circle' and 'the point on the circle'.
• And the distance from the center will be the same for which ever point we take.
An example:
(i) The point with coordinates (1,2) lies on the circle. This is shown in the fig.
(ii) The distance between C and that point = √[(x2-x1)2 + (y2-y1)2]
= √[(1-1)2 + (2-4)2] = √[(0)2 + (-2)2] = √[4] = 2 units
(iii) So 'square of the distance PO' = PO2 = 22= 4
The general case:
1. To write the general case, we consider a circle whose center is at any point C(x1,y1), and radius 'r' units
2. Then square of the distance between the center and any point (x,y) on the circle is:
[(x-x1)2 + (y-y1)2]
• But this distance is the square of the radius which is r2
3. Equating the two, we get:
[(x-x1)2 + (y-y1)2] = r2
• This is the general form of the equation of a circle
• Note the pattern:
♦ x1, which is the x coordinate of the center is subtracted from x
♦ y1, which is the y coordinate of the center is subtracted from y
4. From this we get the general form of the equation of any circle whose center (x1,y1) is at the origin O
• All we need to do is, put x1 = 0 and y1 = 0 in (3)
• Then we get: [x2 + y2] = r2
• This is shown in fig.34.30 below:
 |
| Fig.34.30 |
• The distance from the center of the circle to any point on the circle is indeed '√[x2 + y2]' if the center is at the origin
Now we will see some solved examples:
Solved example 34.16
Find the equation of the line joining (1,2) and (2,4). In this, find the sequence of y coordinates of those points with the consecutive natural numbers 3, 4, 5, . . . as the x coordinates
Solution:
1. Equation of the line joining (1,2) and (2,4):
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (4-2)⁄(2-1) = 2⁄1 = 2
• 'c' of the line = (y1-mx1) = [2 - (2 × 1)] = [2 - 2] = 0
• So equation of the line is
y = mx + c:
y = 2 × x + 0 ⟹ y = 2x
2. We know that the consecutive natural numbers form a sequence. That sequence is:
1, 2, 3, 4, 5, . . .
3. The terms of this sequence form the x coordinates of some points. We can write them as:
(1, _ ), (2, _ ), (3, _ ), (4, _ ), (5, _ ), . . .
4. The y coordinates in the above sequence are left blank. We have to find their values.
• It is given that those y coordinates form a sequence
5. It is easy to find the terms of that sequence. Because we have the equation of the line. It is: y = 2x
• From the equation it is clear that, what ever be the value of x, the value of y will be twice that x value.
• So we can fill up the blank spaces in (3). We get:
(1,2), (2,4), (3,6), (4,8), (5,10), . . .
• Note that, the two points given to us in the question are the first two terms of the sequence.
• The line and the actual positions of the points are shown in the fig.34.31 below:
 |
| Fig.34.31 |
Find the equation of the line joining (-1,3) and (2,5). Prove that if (u,v) is a point on this line, so is (u+3, v+2)
Solution:
1. Equation of the line joining (-1,3) and (2,5)
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (5-3)⁄(2-(-1)) = 2⁄3
• 'c' of the line = (y1-mx1) = [3 - (2⁄3 × -1)] = [3 + 2⁄3] = 11⁄3
• So equation of the line is
y = mx + c:
y = 2⁄3 × x + 11⁄3
2. Given that, (u,v) is a point on the line. What does that mean?
• It simply means that, any point on the line can be taken as (u,v)
• For example, if we consider the point (-1,3), we can take u = -1 and v = 3
• If we consider the point (2,5), we can take u = 2 and v = 5
3. Now we have prove that (u+3, v+2) is also a point on the line.
• For example, we know that (-1,3) is a point on the line.
♦ Then (-1+3, 3+2) should also be a point on the line.
♦ That is., (2,5) should also be a point on the line
• Similarly, we know that (2,5) is a point on the line.
♦ Then (2+3, 5+2) should also be a point on the line.
♦ That is., (5,7) should also be a point on the line
• We have to prove it for the general case.
4. Consider the rough sketch in fig 34.32 below:
 |
| Fig.34.32 |
• The slope of the line joining (u,v) and (u+3, v+2) is
m = (y2-y1)⁄(x2-x1) = (v+2-v)⁄(u+3-u) = 2⁄3
• But this is same slope of the line through (-1,3), (2,5) and (u,v)
• Also, (u,v) is a common point. So (u+3, v+2) will lie in the same line
Solved example 34.18
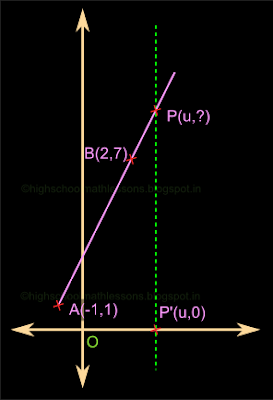
Prove that for any number u, the point (u, 2u+3) is on the line joining (-1,1), (2,7).
Solution:
1. Consider the rough sketch in fig.34.33 below
 |
| Fig.34.33 |
• If we draw a vertical line through that point it will surely meet the given line at some point.
2. Let the marked point P' on the x axis have an x coordinate of 'u'
• Then the meeting point P will also have the x coordinate 'u'
3. The y coordinate of P is not known
■ We have to prove that the y coordinate at the meeting point is:
[(2 times the x coordinate) + 3].
• In other words,
We have to prove that the y coordinate at the meeting point is:
2u+3
4. The equation of a line will help us to find the x coordinate when y coordinate is known
• The equation of a line will also help us to find the y coordinate when the x coordinate is known
5. So let us find the equation of the line:
Equation of the line joining (-1,1) and (2,7)
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (7-1)⁄(2-(-1)) = 6⁄3 = 2
• 'c' of the line = (y1-mx1) = [1 - (2 × -1)] = [1 + 2] = 3
• So equation of the line is
y = mx + c:
y = 2x + 3
6. From the equation it is clear that, at any point, the y coordinate will be:
[(2 times the x coordinate at that point) + 3]
Hence proved
Solved example 34.19
The x coordinate of a point on the slanted line in fig.34.34(a) is 3
 |
| Fig.34.34 |
(ii) What is the slope of the line?
(iii) Write the equation of the line
Solution:
Part (i):
1. Drop a perpendicular from B on to the x axis. Let B' be the foot of the perpendicular. This is shown in fig.b
• So BB' will be the y coordinate of B
2. The ⊿ABB' is a 30o 60o triangle. We can find it's sides using trigonometric properties. (Details here)
• But for that, at least one side of the triangle should be known.
We have:
♦ Length OB' = 3 units
♦ Length OA = 1 unit (since x coordinate of A = 1)
♦ So AB' = 3 - 1 = 2 units
So now we have one side. We can apply the properties of a 30o 60o triangle
• tan 60 = opposite side⁄adjacent side = BB'⁄AB' = BB'⁄2 = √3
⟹ BB' = 2√3
Thus y coordinate of B = BB' = 2√3
Part (ii):
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (2√3-0)⁄(3-1) = (2√3)⁄(2) = √3
Another method:
• If we know the angle θ that a line makes with the horizontal, then the slope of that line is simply tanθ.
• We discussed about it earlier in this chapter. Details here.
• For our present case, slope = tan 60 = √3
Part (iii):
Equation of the line joining (1,0) and (3,2√3)
• Slope of the line = m = √3
• 'c' of the line = (y1-mx1) = [0 - (√3 × 1)] = [0 - √3] = -√3
• So equation of the line is
y = mx + c:
y = √3x - √3 ⟹ y = √3(x-1)
Solved example 34.20
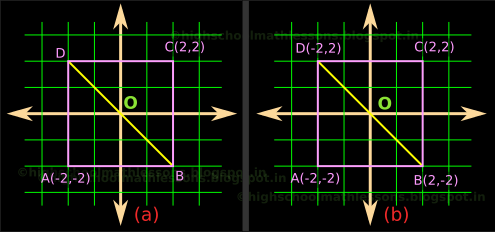
In the fig.34.35(a), ABCD is a square.
 |
| Fig.34.35 |
Solution:
1. The vertices A and C are diagonally opposite. If we are given two such points in a rectangle or a square, we can easily find the coordinates of the other two vertices. Details here.
• So the unknown coordinates at B and D are shown in fig.b
2. Now we have two points on the line BD. We can write the equation
• Equation of the line joining (2,-2) and (-2,2)
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (2-(-2))⁄(-2-2) = 4⁄-2 = -2
• 'c' of the line = (y1-mx1) = [-2 - (-2 × 2)] = [-2 + 4] = 2
• So equation of the line is
y = mx + c:
y = -2x + 2
Solved example 34.21
Prove that for any point on the line intersecting the axes in the fig.34.36 below, the sum of the x and y coordinates is 3
 |
| Fig.30.36 |
1. We have the coordinates of two points on the line.
• Using them we can write the equation of the line
• Equation of the line joining (3,0) and (0,3)
• Slope of the line =
m = (y2-y1)⁄(x2-x1) = (3-0)⁄(0-3) = 3⁄-3 = -1
• 'c' of the line = (y1-mx1) = [0 - (-1 × 3)] = [0 - (-3)] = 3
• So equation of the line is
y = mx + c:
y = -1x + 3
2. From this equarion we get: x+y = 3
That is., for every point on this line, the sum of x and y coordinates will be 3
Solved example 34.22
Find the equation of the circle with center at the origin and radius 5 cm. Write the coordinates of 8 points on this circle
Solution:
1. We have seen at the beginning of this section that:
Equation of a circle with center O and radius r is
[x2 + y2] = r2.
• So for our present case, the equation is: [x2 + y2] = 52 ⟹ [x2 + y2] = 25
2. The circle cuts the axes at the following four points:
(i) P at the positive side of the x axis
(ii) P' at the negative side of the x axis
(iii) Q at the positive side of the y axis
(ii) Q' at the negative side of the y axis
These are shown in the fig.34.37(a) below:
 |
| Fig.34.37 |
(i) Point P: Since the point P is on the x axis, the y coordinate will be equal to zero.
• So put y = 0 in the equation of the circle in (1)
• We get: [x2 + 0] = 25 ⟹ x2 = 25 ⟹ x = √25 = ±5
• There will be two roots for 25. They are +5 and -5.
• That means, the circle will intersect with the x axis at two points.
♦ One point is P on the positive side of the x axis. The coordinates are (5,0)
♦ The other point P' is on the negative side of the x axis. The coordinates are (-5,0)
• This is shown in the fig.30.37(a) above
• So we started out to find P and got both P and P'
(ii) Point P': This is already obtained above
(iii) Point Q: Since the point Q is on the y axis, the x coordinate will be equal to zero.
• So put x = 0 in the equation of the circle in (1)
• We get: [0 + y2] = 25 ⟹ y2 = 25 ⟹ y = √25 = ±5
• There will be two roots for 25. They are +5 and -5.
• That means, the circle will intersect with the y axis at two points.
♦ One point Q is on the positive side of the y axis. The coordinates are (0,5)
♦ The other point Q' is on the negative side of the y axis. The coordinates are (0,-5)
• This is shown in the fig.30.37(a) above
• So we started out to find Q and got both Q and Q'
(ii) Point Q': This is already obtained above
3. We want four more points.
• For that, we draw a line at an angle of 60o with the positive side of the x axis.
♦ This line meets the circle at R. This is shown in fig.34.37(b) above
• A perpendicular is dropped from R on to the x axis. The foot of the perpendicular is R'
♦ Now x coordinate of R will be equal to OR'
♦ y coordinate of R will be equal to RR'
• This is a problem similar to solved example 34.19 that we saw above. In that problem we used the trigonometrical ratio tan. In this example we will use sine and cosine
Consider ⊿ORR'. We have:
• sin 60 = opposite side⁄hypotenuse = RR'⁄OR = RR'⁄5
But from the tables, sin 60 = √3⁄2
So we can write: RR'⁄5 = √3⁄2 ⟹ RR' = (5√3)⁄2
• cos 60 = adjacent side ⁄hypotenuse = OR'⁄OR = OR'⁄5
But from the tables, cos 60 = 1⁄2
So we can write: OR'⁄5 = 1⁄2 ⟹ OR' = 5⁄2
Thus the coordinates of R are: [5⁄2 , (5√3)⁄2]
Check:
• Applying Pythagoras theorem in ⊿ORR', we have:
OR = √[(OR')2 + (RR')2] = √[(5⁄2)2 + ((5√3)⁄2)2] = √[25⁄4 + 75⁄4] = √[100⁄4] = √[25] = 5 units
• The radius is given as 5 cm. So our calculations are correct
4. Three more points can be obtained in the same way. They are: S, S'' and R''. They are shown in fig.b. They are symmetrical to the point R that we calculated above. So the coordinates can be written easily:
Point S: [-5⁄2 , (5√3)⁄2]
Point S'': [-5⁄2 , (-5√3)⁄2]
Point R'': [5⁄2 , (-5√3)⁄2]
Solved example 34.23
Let (x,y) be a point on the circle with the line joining (0,1) and (2,3) as diameter.
(i) Prove that x2+ y2 - 2x - 4y +3 = 0.
(ii) Find the coordinates of the points where the circle cuts the x axis
Solution:
1. The end points of a diameter are (0,1) and (2,3)
From this we get:
• x coordinate of the midpoint = (x1+x2)⁄2 = (0+2)⁄2 = 2⁄2 = 1
• y coordinate of the midpoint = (y1+y2)⁄2 = (1+3)⁄2 = 4⁄2 = 2
• So the coordinates of the midpoint are (Details here): (1,2)
• But the midpoint of the diameter is same as the center of the circle
2. Length of the diameter can be calculated using the distance formula:
Diameter = √[(x2-x1)2 + (y2-y1)]2 = √[(2-0)2 + (3-1)2] = √[(2)2 + (2)2] = √8 = √[2×4] = 2√2
• So radius = (2√2)⁄2 = √2 units
3. The general form of the equation of any circle whose center is at any point C(x1,y1), and radius is 'r' units is: [(x-x1)2 + (y-y1)2] = r2.
• So we get the equation of our circle:
[(x-1)2 + (y-2)2] = (√2)2.
• Expanding the above expression, we get:
x2 -2x + 1 + y2 - 4y + 4 = 2 ⟹ x2+ y2 - 2x - 4y +3 = 0
Part (ii):
1. At the points where the circle cuts the x axis, the y coordinates will be zero.
2. So we can put y = 0 in the equation of the circle:
x2+ 02 - 2x - 4×0 +3 = 0 ⟹ x2 - 2x +3 = 0
3. This is of the form ax2 + bx + c = 0 (Details here)
Where: a = 1, b = (-2) and c = 3
4. So we can use the general formula to solve the equation
5. b2-4ac = (-2)2-4×1×3 = 4 - 12 = -8
• This is a negative quantity.
• This is a negative quantity.
• So '√[b2-4ac]' cannot be calculated
• The equation does not have a solution. That means, the circle never crosses the x axis.
• The actual positions in the Cartesian plane are shown in the fig.34.38 below:
• Note that the radius is √2 units. It is difficult to mark the value of √2 precisely on the x or y axis
• But we have seen the methods to draw a line of length √2 geometrically (Details here)
• Using a graph paper, it is even more easier because, √2 is the diagonal of a square of side 1 unit
Solved example 34.24
What is the equation of the circle in the fig.34.39 below?• The equation does not have a solution. That means, the circle never crosses the x axis.
• The actual positions in the Cartesian plane are shown in the fig.34.38 below:
 |
| Fig.34.38 |
• But we have seen the methods to draw a line of length √2 geometrically (Details here)
• Using a graph paper, it is even more easier because, √2 is the diagonal of a square of side 1 unit
Solved example 34.24
 |
| Fig.34.39 |
• We know that, the axes are always perpendicular to each other
• In this problem, the point of intersection of the axes, that is., the origin, lies on the circle
• So AB will be a diameter of the circle (Details here)
1. The end points of a diameter are (0,2) and (4,0)
From this we get:
• x coordinate of the midpoint = (x1+x2)⁄2 = (0+4)⁄2 = 4⁄2 = 2
• y coordinate of the midpoint = (y1+y2)⁄2 = (2+0)⁄2 = 2⁄2 = 1
• So the coordinates of the midpoint are (Details here): (2,1)
• But the midpoint of the diameter is same as the center of the circle
2. Length of the diameter can be calculated using the distance formula:
Diameter = √[(x2-x1)2 + (y2-y1)]2 = √[(4-0)2 + (0-2)2] = √[(4)2 + (-2)2] = √20 = √[5×4] = 2√5
• So radius = (2√5)⁄2 = √5 units
3. The general form of the equation of any circle whose center is at any point C(x1,y1), and radius is 'r' units is: [(x-x1)2 + (y-y1)2] = r2.
• So we get the equation of our circle:
[(x-2)2 + (y-1)2] = (√5)2.
• Expanding the above expression, we get:
x2 -4x + 4 + y2 - 2y + 1 = 5 ⟹ x2+ y2 - 4x - 2y = 0

No comments:
Post a Comment