In the previous section we completed a discussion about median. In this section we will see Ogive curves.
• We know that one picture can replace a thousand words. We have seen examples of this in our previous discussions in statistics (part II). There we saw bar graphs, histograms, frequency polygons etc.,
• We saw that those graphs help to get an understanding about the data at a glance.
• In our present discussion, we have not yet drawn any graphs. So let us try to 'represent pictorially', what we have learned so far in this chapter. We will write it in steps:
1. Consider the table 37.39 that we saw earlier. It is shown again below:
• Let us plot the cumulative frequencies along the y axis
• Then the class intervals will be plotted along the x axis
• But we see that each class interval has two values: a lower limit and an upper limit. Which one will we use for plotting?
2. Let us choose the upper limits
• Then the coordinates of the points on the graphs will be:
(10,5), (20,8), (30,12), (40,15), . . . , (100,53)
• The graph thus obtained is shown in fig.37.1 below:
• Note that the scale need not be the same for both the axes
• The curve (shown in magenta colour) joining the points is called a cumulative frequency curve or an ogive
3. So we know how to draw an ogive. Let us now see it's features:
• Suppose we want to know the cumulative frequency corresponding to a class 70-80
• Then we take the point on the graph at which the x coordinate is 80
• At that point, the y coordinate is 38.
• That means the cumulative frequency at that point is 38
• So the cumulative frequency corresponding to class 70-80 is 38
• That means, 38 observations in the given data have a value lesser than 80
4. In our present example, the observations are: 'marks obtained by 53 students'
• So we can write:
38 students have marks less than 80
• If the observations are 'weights', we can write:
38 students have weights less than 80 kg
• If the observations are 'lengths of leaves', we can write:
38 leaves have length less than 80 mm'
5. So it is a convenient way to get a quick understanding about the data
• Note that we use less than 80. This is because, if there is a mark equal to 80, it will not be included in the class 70-80. It will be included only in 80-90
• So all marks equal to and greater than 80 will be on the right side of (80,38)
6. So which ever point we consider in the graph in fig.37.1 above, we get valuable information. We will break down the information as follows:
(i) The coordinates of the point will be in the form: (x coordinate, y coordinate)
(ii) 'y coordinate' number of students have scored less than 'x coordinate' marks
An example:
• Take class mark 50 on the x axis
• The y coordinate corresponding to it is 18. So we have: (50,18)
■ We can write:
18 students have scored less than 50 marks
7. So the graph in fig.37.1 is marked as 'Less than ogive'
8. (80, 38) and (50,18) are points already written on the ogive. We can get information on other points also:
(i) Consider the score 75. We want to know how many students got less than 75
(ii) For that, mark a point R at (75,0) on the x axis.
(iii) Draw a vertical dashed line (shown in white colour in fig.37.2 below) through R
(iv) Let it intersect the ogive at Q
(v) Draw a horizontal white dashed line through Q
(vi) Let it intersect the y axis at P
(vii) Note down the 'y coordinate' of P. It is 33.5
• We can write:
About 33 students have scored less than 75 marks
• Note that, if we are using a graph paper, we will not need to draw the dashed lines. They will be already present in the form of thin lines.
So we have seen the Less than ogive. Is there a 'More than ogive' ? Let us see:
1. Consider the table 37.40 that we saw earlier. It is from the same problem. It is shown again below:
Draw both ogives for the data above. Hence obtain the median profit.
Solution:
1. We are given a cumulative frequency table.
• The cumulative frequencies in the second column can be used to draw the more than ogive. But those cumulative frequencies will give only the y coordinates of the points.
• To know the x coordinates, we need class intervals.
2. So we will convert the given 'cumulative frequency distribution table' into a 'grouped frequency distribution table':
• Consider the first row of the given table:
All the shops are making a profit of more than or equal to 5 lakhs
• Consider the second row of the given table:
28 shops are making a profit of more than or equal to 10 lakhs
• 'More than or equal to 10' will include 'more than or equal to 5' also
• So number of shops making a profit of more than 5 lakhs but less than 10 lakhs is (30-28) = 2
• So the frequency corresponding to class 5-10 will be 2
• This is shown in the first row of our new table 37.54 below
3. Consider the third row of the given table:
• 16 shops are making a profit of more than or equal to 15 lakhs
• 'More than or equal to 15' will include 'more than or equal to 10' also
• So number of shops making a profit of more than 10 lakhs but less than 15 lakhs is (28-16) = 12
• So the frequency corresponding to class 10-15 will be 12
• This is shown in the second row of our new table 37.54 below
4. Consider the fourth row of the given table:
• 14 shops are making a profit of more than or equal to 20 lakhs
• 'More than or equal to 20' will include 'more than or equal to 15' also
• So number of shops making a profit of more than 15 lakhs but less than 20 lakhs is (16-14) = 2
• So the frequency corresponding to class 15-20 will be 2
• This is shown in the third row of our new table 37.54 below
In this way we can continue up to the last row. But once we understand the pattern, the columns can be easily filled up.
5. Now we can draw the ogives.
(i) First we will draw the less than ogive.
• We know that, for the less than ogive, the x coordinates are the upper limits of the class intervals
• y coordinates are the cumulative frequencies of the less than type. This is given in the third column of the above table 37.53
♦ As usual, this column is easily filled up using the pattern
• So the coordinates will be: (10,2), (15,14), (20,16), . . . , (40,30)
• The curve joining these points is the less than ogive of this problem. It is shown in magenta colour in fig.37.7 below:
• A sample:
♦ (30,23) is a point on the less than ogive
♦ So there are 23 shops which make a profit of less than 23 lakhs
(ii) Now we will draw the more than ogive.
• We know that, for the more than ogive, the x coordinates are the lower limits of the class intervals
• y coordinates are the cumulative frequencies of the more than type. They were given to us in the question. They are shown again in the fourth column of the above table 37.53
• So the coordinates will be: (5,30), (10,28), (15,16), . . . , (35,3)
• The curve joining these points is the more than ogive of this problem. It is shown in yellow colour in fig.37.7 above.
• A sample:
♦ (25,10) is a point on the more than ogive
♦ So there are 10 shops which make a profit of more than 25 lakhs
6. To find the median:
• Let the two ogives intersect at Q. From Q, draw a vertical dashed line. It will intersect the x axis at R
• The coordinates of R are (17.5,0)
• So the median profit is 17.5 lakhs
• Note that, the y coordinate of Q is 15.
♦ This 15 is equal to (n⁄2) = (30⁄2)
7. Conclusion:
• If we arrange all the 30 shops in the increasing order of profit, the shop which makes a profit of 17.5 lakhs will come in the middle.
• There will be about 15 shops on the left of this shop. Each of their profits will be less than 17.5 lakhs
• There will be about 15 shops on the right of this shop. Each of their profits will be more than 17.5 lakhs
The term ‘ogive’ is pronounced as ‘ojeev’ and is derived from the word 'ogee'. An ogee is a curved shape consisting of concave and convex arcs. It was used to form arches of buildings in the 14th and 15th century Gothic styles. Our ogive curves in statistics resemble those curves, and so the name was given.
In the next section, we will see some solved examples.
The link below gives the notes on statistics of class 11:
Mean deviation and Standard deviation.
• We know that one picture can replace a thousand words. We have seen examples of this in our previous discussions in statistics (part II). There we saw bar graphs, histograms, frequency polygons etc.,
• We saw that those graphs help to get an understanding about the data at a glance.
• In our present discussion, we have not yet drawn any graphs. So let us try to 'represent pictorially', what we have learned so far in this chapter. We will write it in steps:
1. Consider the table 37.39 that we saw earlier. It is shown again below:
 |
| Table.37.39 |
• Then the class intervals will be plotted along the x axis
• But we see that each class interval has two values: a lower limit and an upper limit. Which one will we use for plotting?
2. Let us choose the upper limits
• Then the coordinates of the points on the graphs will be:
(10,5), (20,8), (30,12), (40,15), . . . , (100,53)
• The graph thus obtained is shown in fig.37.1 below:
 |
| Fig.37.1 |
• The curve (shown in magenta colour) joining the points is called a cumulative frequency curve or an ogive
3. So we know how to draw an ogive. Let us now see it's features:
• Suppose we want to know the cumulative frequency corresponding to a class 70-80
• Then we take the point on the graph at which the x coordinate is 80
• At that point, the y coordinate is 38.
• That means the cumulative frequency at that point is 38
• So the cumulative frequency corresponding to class 70-80 is 38
• That means, 38 observations in the given data have a value lesser than 80
4. In our present example, the observations are: 'marks obtained by 53 students'
• So we can write:
38 students have marks less than 80
• If the observations are 'weights', we can write:
38 students have weights less than 80 kg
• If the observations are 'lengths of leaves', we can write:
38 leaves have length less than 80 mm'
5. So it is a convenient way to get a quick understanding about the data
• Note that we use less than 80. This is because, if there is a mark equal to 80, it will not be included in the class 70-80. It will be included only in 80-90
• So all marks equal to and greater than 80 will be on the right side of (80,38)
6. So which ever point we consider in the graph in fig.37.1 above, we get valuable information. We will break down the information as follows:
(i) The coordinates of the point will be in the form: (x coordinate, y coordinate)
(ii) 'y coordinate' number of students have scored less than 'x coordinate' marks
An example:
• Take class mark 50 on the x axis
• The y coordinate corresponding to it is 18. So we have: (50,18)
■ We can write:
18 students have scored less than 50 marks
7. So the graph in fig.37.1 is marked as 'Less than ogive'
8. (80, 38) and (50,18) are points already written on the ogive. We can get information on other points also:
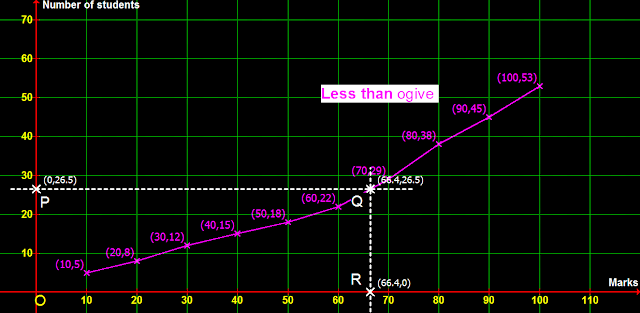
(i) Consider the score 75. We want to know how many students got less than 75
(ii) For that, mark a point R at (75,0) on the x axis.
(iii) Draw a vertical dashed line (shown in white colour in fig.37.2 below) through R
 |
| Fig.37.2 |
(v) Draw a horizontal white dashed line through Q
(vi) Let it intersect the y axis at P
(vii) Note down the 'y coordinate' of P. It is 33.5
• We can write:
About 33 students have scored less than 75 marks
• Note that, if we are using a graph paper, we will not need to draw the dashed lines. They will be already present in the form of thin lines.
So we have seen the Less than ogive. Is there a 'More than ogive' ? Let us see:
1. Consider the table 37.40 that we saw earlier. It is from the same problem. It is shown again below:
 |
| Table.37.40 |
• Let us plot the cumulative frequencies along the y axis
• Then the class intervals will be plotted along the x axis
• But we see that each class interval has two values: a lower limit and an upper limit. Which one will we use for plotting?
2. Let us choose the lower limits
• Then the coordinates of the points on the graphs will be:
(0,53), (10,48), (20,45), (30,41), . . . , (90,8)
• The graph thus obtained is shown in fig.37.3 below:
• Note that the scale need not be the same for both the axes
• The curve (shown in yellow colour) joining the points is a cumulative frequency curve or an ogive
3. So we know how to draw this new type of ogive also. Let us now see it's features:
• Suppose we want to know the cumulative frequency corresponding to a class 70-80
• Then we take the point on the graph at which the x coordinate is 70
• At that point, the y coordinate is 24.
• That means the cumulative frequency at that point is 24
• So the cumulative frequency corresponding to class 70-80 is 24
• That means, 24 observations in the given data have a value more than 70
4. In our present example, the observations are: marks obtained by 53 students
• So we can write:
24 students have marks more than 70
• If the observations are 'weights', we can write:
24 students have weights more than 70 kg
• If the observations are 'lengths of leaves', we can write:
24 leaves have length more than 70 mm
5. So it is a convenient way to get a quick understanding about the data
• Note that we use more than 70.
6. So which ever point we consider in the graph in fig.37.2 above, we get valuable information. We will break down the information as follows:
(i) The coordinates of the point will be in the form: (x coordinate, y coordinate)
(ii) 'y coordinate' number of students have scored more than 'x coordinate' marks
An example:
• Take class mark 50 on the x axis
• The y coordinate corresponding to it is 35. So we have: (50,35)
■ We can write:
35 students have scored more than 50 marks
7. So the graph in fig.37.3 is marked as 'More than ogive'
8. (70, 24) and (50,35) are points already written on the ogive. We can get information on other points also.
• For that, draw the required vertical and horizontal dashed lines just as we saw in the case of less than ogive.
Now we will see an interesting application of the 'less than ogive'. We will write it in steps:
1. In fig.37.2 above, we started to work from point R which is on the x axis.
• Then we reached Q and then finally P, which is on the y axis.
• The point P gave us the 'number of students'
2. How about working in a reverse order?
• If we start from a point P on the y axis, we will be starting with a 'particular number of students'
• When we reach the x axis, we will get a 'particular score' Q
• The no. of students at P will have scored less than the marks at Q
3. Do we have any 'particular number of students' which might be of interest?
• We certainly do.
• 'Half the number' is often an important point in any data. It is related to 'the median'
• In our present case, the median is (53⁄2) = 26.5
4. So we mark P (0,26.5) on the y axis and start from there. The path to R on the x axis is shown in fig.37.4 below:
• We get R (66.4,0). So we can write:
About 26 students scored less than 66.4 The other 26 scored more than 66.4
• In other words, 66.4 is the median score
■ So it is clear: To find the median, mark (0,n⁄2) on the y axis and work towards the x axis
5. We proved it using a less than ogive. Will it work on a more than ogive?
The path from P to R is marked on the more than ogive in fig.37.5 below:
• We get the same result: The median is 66.4
7. So it means that point Q has the same coordinates in both less than and more than ogives
That is., Q is common in both the curves
In other words, Q is the point of intersection of the two curves. This is shown in the fig.37.6 below:
8. So, instead finding (n⁄2) and then drawing horizontal and vertical dashed lines, we can do the following steps:
(i) Draw both the ogives
(ii) Mark the point of intersection Q
(iii) Draw a vertical dashed line through Q. Let it meet the x axis at R
(iv) then the x coordinate of R is the median
An example:
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution :
• Then the class intervals will be plotted along the x axis
• But we see that each class interval has two values: a lower limit and an upper limit. Which one will we use for plotting?
2. Let us choose the lower limits
• Then the coordinates of the points on the graphs will be:
(0,53), (10,48), (20,45), (30,41), . . . , (90,8)
• The graph thus obtained is shown in fig.37.3 below:
 |
| Fig.37.3 |
• The curve (shown in yellow colour) joining the points is a cumulative frequency curve or an ogive
3. So we know how to draw this new type of ogive also. Let us now see it's features:
• Suppose we want to know the cumulative frequency corresponding to a class 70-80
• Then we take the point on the graph at which the x coordinate is 70
• At that point, the y coordinate is 24.
• That means the cumulative frequency at that point is 24
• So the cumulative frequency corresponding to class 70-80 is 24
• That means, 24 observations in the given data have a value more than 70
4. In our present example, the observations are: marks obtained by 53 students
• So we can write:
24 students have marks more than 70
• If the observations are 'weights', we can write:
24 students have weights more than 70 kg
• If the observations are 'lengths of leaves', we can write:
24 leaves have length more than 70 mm
5. So it is a convenient way to get a quick understanding about the data
• Note that we use more than 70.
6. So which ever point we consider in the graph in fig.37.2 above, we get valuable information. We will break down the information as follows:
(i) The coordinates of the point will be in the form: (x coordinate, y coordinate)
(ii) 'y coordinate' number of students have scored more than 'x coordinate' marks
An example:
• Take class mark 50 on the x axis
• The y coordinate corresponding to it is 35. So we have: (50,35)
■ We can write:
35 students have scored more than 50 marks
7. So the graph in fig.37.3 is marked as 'More than ogive'
8. (70, 24) and (50,35) are points already written on the ogive. We can get information on other points also.
• For that, draw the required vertical and horizontal dashed lines just as we saw in the case of less than ogive.
Now we will see an interesting application of the 'less than ogive'. We will write it in steps:
1. In fig.37.2 above, we started to work from point R which is on the x axis.
• Then we reached Q and then finally P, which is on the y axis.
• The point P gave us the 'number of students'
2. How about working in a reverse order?
• If we start from a point P on the y axis, we will be starting with a 'particular number of students'
• When we reach the x axis, we will get a 'particular score' Q
• The no. of students at P will have scored less than the marks at Q
3. Do we have any 'particular number of students' which might be of interest?
• We certainly do.
• 'Half the number' is often an important point in any data. It is related to 'the median'
• In our present case, the median is (53⁄2) = 26.5
4. So we mark P (0,26.5) on the y axis and start from there. The path to R on the x axis is shown in fig.37.4 below:
 |
| Fig.37.4 |
About 26 students scored less than 66.4 The other 26 scored more than 66.4
• In other words, 66.4 is the median score
■ So it is clear: To find the median, mark (0,n⁄2) on the y axis and work towards the x axis
5. We proved it using a less than ogive. Will it work on a more than ogive?
The path from P to R is marked on the more than ogive in fig.37.5 below:
 |
| Fig.37.5 |
7. So it means that point Q has the same coordinates in both less than and more than ogives
That is., Q is common in both the curves
In other words, Q is the point of intersection of the two curves. This is shown in the fig.37.6 below:
 |
| Fig.37.6 |
(i) Draw both the ogives
(ii) Mark the point of intersection Q
(iii) Draw a vertical dashed line through Q. Let it meet the x axis at R
(iv) then the x coordinate of R is the median
An example:
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution :
 |
| Table.37.53 |
Solution:
1. We are given a cumulative frequency table.
• The cumulative frequencies in the second column can be used to draw the more than ogive. But those cumulative frequencies will give only the y coordinates of the points.
• To know the x coordinates, we need class intervals.
2. So we will convert the given 'cumulative frequency distribution table' into a 'grouped frequency distribution table':
• Consider the first row of the given table:
All the shops are making a profit of more than or equal to 5 lakhs
• Consider the second row of the given table:
28 shops are making a profit of more than or equal to 10 lakhs
• 'More than or equal to 10' will include 'more than or equal to 5' also
• So number of shops making a profit of more than 5 lakhs but less than 10 lakhs is (30-28) = 2
• So the frequency corresponding to class 5-10 will be 2
• This is shown in the first row of our new table 37.54 below
3. Consider the third row of the given table:
• 16 shops are making a profit of more than or equal to 15 lakhs
• 'More than or equal to 15' will include 'more than or equal to 10' also
• So number of shops making a profit of more than 10 lakhs but less than 15 lakhs is (28-16) = 12
• So the frequency corresponding to class 10-15 will be 12
• This is shown in the second row of our new table 37.54 below
4. Consider the fourth row of the given table:
• 14 shops are making a profit of more than or equal to 20 lakhs
• 'More than or equal to 20' will include 'more than or equal to 15' also
• So number of shops making a profit of more than 15 lakhs but less than 20 lakhs is (16-14) = 2
• So the frequency corresponding to class 15-20 will be 2
• This is shown in the third row of our new table 37.54 below
 |
| Table.37.54 |
5. Now we can draw the ogives.
(i) First we will draw the less than ogive.
• We know that, for the less than ogive, the x coordinates are the upper limits of the class intervals
• y coordinates are the cumulative frequencies of the less than type. This is given in the third column of the above table 37.53
♦ As usual, this column is easily filled up using the pattern
• So the coordinates will be: (10,2), (15,14), (20,16), . . . , (40,30)
• The curve joining these points is the less than ogive of this problem. It is shown in magenta colour in fig.37.7 below:
 |
| Fig.37.7 |
♦ (30,23) is a point on the less than ogive
♦ So there are 23 shops which make a profit of less than 23 lakhs
(ii) Now we will draw the more than ogive.
• We know that, for the more than ogive, the x coordinates are the lower limits of the class intervals
• y coordinates are the cumulative frequencies of the more than type. They were given to us in the question. They are shown again in the fourth column of the above table 37.53
• So the coordinates will be: (5,30), (10,28), (15,16), . . . , (35,3)
• The curve joining these points is the more than ogive of this problem. It is shown in yellow colour in fig.37.7 above.
• A sample:
♦ (25,10) is a point on the more than ogive
♦ So there are 10 shops which make a profit of more than 25 lakhs
6. To find the median:
• Let the two ogives intersect at Q. From Q, draw a vertical dashed line. It will intersect the x axis at R
• The coordinates of R are (17.5,0)
• So the median profit is 17.5 lakhs
• Note that, the y coordinate of Q is 15.
♦ This 15 is equal to (n⁄2) = (30⁄2)
7. Conclusion:
• If we arrange all the 30 shops in the increasing order of profit, the shop which makes a profit of 17.5 lakhs will come in the middle.
• There will be about 15 shops on the left of this shop. Each of their profits will be less than 17.5 lakhs
• There will be about 15 shops on the right of this shop. Each of their profits will be more than 17.5 lakhs
The term ‘ogive’ is pronounced as ‘ojeev’ and is derived from the word 'ogee'. An ogee is a curved shape consisting of concave and convex arcs. It was used to form arches of buildings in the 14th and 15th century Gothic styles. Our ogive curves in statistics resemble those curves, and so the name was given.
The link below gives the notes on statistics of class 11:
Mean deviation and Standard deviation.
CyusInternationalBest manufacturer and exporter of a wide range of Oil Seals, O Rings, Piston Seals, Rod Seals, O Ring Cord, and much more are available at lowest prices in Faridabad. If you Looking for Bulk Order. Contact Now
ReplyDeletepujasealsPuja Fluid Seals Pvt. Ltd. is a Industrial Rubber Products Manufacturer in India. If you Looking for Bulk Order. Contact Now
ReplyDelete