In the previous section we learned the construction of Non Isosceles Trapezium. We have also learned about Isosceles Trapezium, Rhombus and Parallelogram. They are all Quadrilaterals with definite shapes. In this section, we will learn the construction of Quadrilaterals in general.
Fig.(i) shows the quadrilateral ABCD with the given sides. Fig.(ii) also shows a quadrilateral with the same sides. (Note that, both (i) and (ii) are actual constructions. They are not rough sketches). It is clear that the two quadrilaterals are entirely different from each other. This is because, the angle at A is different. In fig.(i) ∠A = 70o, and in fig.(ii) ∠A = 50o. So, to define a quadrilateral, we will need the lengths of all the four sides and the measurement of at least one interior angle.
Solved example 12.13
Construct the quadrilateral ABCD shown in fig.12.21(i)
Solution:
• Draw a horizontal line AB 6 cm in length
• Draw a line AD’ at an angle of 70o with AB. The corner D lies on this line at a distance of 5 cm from A
• With A as center, draw an arc (shown in yellow colour in fig. 12.22a) of radius 5 cm, cutting AD’ At D.
• So we have obtained the three corners A, B and D. We have to locate the remaining corner C
• C is at a distance of 4 cm from D and 3 cm from B. So, with D as center, draw an arc (shown in green colour in fig. 12.22b) of radius 4 cm. With B as center, draw an arc (shown in magenta colour in fig.12.22b) of radius 3 cm
• These two arcs intersect at point C. Join DC and CB. Thus we get the required quadrilateral ABCD
Solved example 12.14
Construct the quadrilateral ABCD shown in fig.12.21(ii)
Solution:
• Draw a horizontal line AB 6 cm in length
• Draw a line AD’ at an angle of 50o with AB. The corner D lies on this line at a distance of 5 cm from A
• With A as center, draw an arc (shown in yellow colour in fig. 12.23a) of radius 5 cm, cutting AD’ At D.
• So we have obtained the three corners A, B and D. We have to locate the remaining corner C
• C is at a distance of 4 cm from D and 3 cm from B. So, with D as center, draw an arc (shown in green colour in fig. 12.23b) of radius 4 cm. With B as center, draw an arc (shown in magenta colour in fig.12.23b) of radius 3 cm
• These two arcs intersect at point C. Join DC and CB. Thus we get the required quadrilateral ABCD
Solved example 12.15
Construct a quadrilateral ABCD in which AB = 5.1 cm, BC = 2.4 cm, CD = 6.9 cm, DA = 4.0 cm, and Diagonal AC = 6.6 cm
Solution: In this problem, the lengths of all the four sides are given. But the interior angle is missing. Instead, we are given the length of a diagonal. With these details, we can indeed draw the quadrilateral. The first step is to draw a rough sketch as shown in fig.12.24(a)
From the rough sketch it is clear that, the diagonal splits the quadrilateral ABCD into two triangles: ΔABC and ΔADC. The lengths of all the sides of these triangles are known. So it is a simple case of ‘construction of two triangles’.
• Draw a horizontal line AB, 5.1 cm in length
• With A as center, draw an arc (shown in white colour in fig.b) of radius 6.6 cm. With B as center, draw an arc (shown in magenta colour in fig.b) of radius 2.4 cm
• These two arcs will intersect at C. Join B and C. So we have obtained three corners, A, B and C of the Quadrilateral. Now we have to locate the remaining corner D
• With A as center, draw an arc (shown in green colour in fig.c) of radius 4.0 cm. With C as center, draw an arc (shown in yellow colour in fig.c) of radius 6.9 cm
• These two arcs will intersect at D. Join A to D and C to D. Thus we get the required quadrilateral ABCD
Solved example 12.16
Construct a quadrilateral ABCD in which AB = 5.4 cm, BC = 4.0 cm, CD = 6.2 cm, ∠B = 105o, and ∠C = 70o
Solution: In this problem, the lengths of only three sides are given. Also no diagonal is given. Instead, two interior angles are given. With these details, we can indeed draw the quadrilateral. The first step is to draw a rough sketch as shown in fig.12.25(a)
• Draw a horizontal line AB, 5.4 cm in length
• Draw line BC’ at an angle of 105o with AB
• With B as center, draw an arc (shown in magenta colour in fig.b) of radius 4 cm. This arc cuts BC’ at C. So we have obtained three corners A, B and C. We have to locate the remaining corner D
• Draw a line CD’ at an angle of 70o with BC.
• With C as center, draw an arc (shown in yellow colour in fig.c) of radius 6.2 cm. This arc cuts CD’ at D. Join A to D. Thus we get the required quadrilateral ABCD
Solved example 12.17
Construct a quadrilateral ABCD in which AB = 7.4 cm, BC = 4.3 cm, ∠A = 86o, ∠B = 47o, and ∠C = 151o
Solution: In this problem, the lengths of only three sides are given. Also no diagonal is given. Instead, two interior angles are given. With these details, we can indeed draw the quadrilateral. The first step is to draw a rough sketch as shown in fig.12.26(a)
• Draw a horizontal line AB, 7.4 cm in length
• Draw line BC’ at an angle of 47o with AB
• With B as center, draw an arc (shown in yellow colour in fig.b) of radius 4.3 cm. This arc cuts BC’ at C. So we have obtained three corners A, B and C. We have to locate the remaining corner D
• Draw a line CD’ at an angle of 151o with BC
• Draw a line AD at an angle of 86o with AB. This line intersects CD' at D. Thus we get the required quadrilateral ABCD
Solved example 12.18
Construct a quadrilateral ABCD in which AB = 6.0 cm, BC = 5.5 cm, AD = 3.2 cm, Diagonal AC = 6.2 cm, and diagonal BD = 5.0 cm
Solution: In this problem, the lengths of three sides, and two diagonals are given. With these details, we can indeed draw the quadrilateral. The first step is to draw a rough sketch as shown in fig.12.24(a)
From the rough sketch, we have to pick out two triangles, whose all three sides are known. There are two such triangles: ΔABD and ΔABC. Note that, we cannot pick ΔACD because, one of it’s sides CD is an unknown. So we use ΔABD and ΔABC for the construction:
• Draw a horizontal line AB, 6.0 cm in length
• With A as center, draw an arc (shown in magenta colour in fig.b) of radius 3.2 cm. With B as center, draw an arc (shown in yellow colour in fig.b) of radius 5.0 cm
• These two arcs will intersect at D. Join A and D. So we have obtained three corners, A, B and D of the Quadrilateral. Now we have to locate the remaining corner C
• With A as center, draw an arc (shown in yellow colour in fig.c) of radius 6.2 cm. With B as center, draw an arc (shown in green colour in fig.c) of radius 5.5 cm
• These two arcs will intersect at C. Join B to C and C to D. Thus we get the required quadrilateral ABCD
So we have learned to construct a Quadrilateral under five conditions:
■ When the lengths of all the sides and one interior angle are given
■ When the lengths of all the sides and one diagonal are given
■ When the lengths of three sides and two interior angles are given
■ When the lengths of two sides and three interior angles are given
■ When the lengths of three sides and two diagonals are given
In the next section, we will learn the calculation of Areas of Quadrilaterals.
Construction of Quadrilaterals
Consider a Quadrilateral ABCD having sides 6, 3, 4 and 5 cm. We know that a quadrilateral have four sides. But, just with the lengths of those four sides, a quadrilateral cannot be defined. It requires one more parameter. Look at the fig.12.21 given below: |
| Fig.12.21 |
Solved example 12.13
Construct the quadrilateral ABCD shown in fig.12.21(i)
Solution:
 |
| Fig.12.22 |
• Draw a line AD’ at an angle of 70o with AB. The corner D lies on this line at a distance of 5 cm from A
• With A as center, draw an arc (shown in yellow colour in fig. 12.22a) of radius 5 cm, cutting AD’ At D.
• So we have obtained the three corners A, B and D. We have to locate the remaining corner C
• C is at a distance of 4 cm from D and 3 cm from B. So, with D as center, draw an arc (shown in green colour in fig. 12.22b) of radius 4 cm. With B as center, draw an arc (shown in magenta colour in fig.12.22b) of radius 3 cm
• These two arcs intersect at point C. Join DC and CB. Thus we get the required quadrilateral ABCD
Solved example 12.14
Construct the quadrilateral ABCD shown in fig.12.21(ii)
Solution:
 |
| Fig.12.23 |
• Draw a line AD’ at an angle of 50o with AB. The corner D lies on this line at a distance of 5 cm from A
• With A as center, draw an arc (shown in yellow colour in fig. 12.23a) of radius 5 cm, cutting AD’ At D.
• So we have obtained the three corners A, B and D. We have to locate the remaining corner C
• C is at a distance of 4 cm from D and 3 cm from B. So, with D as center, draw an arc (shown in green colour in fig. 12.23b) of radius 4 cm. With B as center, draw an arc (shown in magenta colour in fig.12.23b) of radius 3 cm
• These two arcs intersect at point C. Join DC and CB. Thus we get the required quadrilateral ABCD
Solved example 12.15
Construct a quadrilateral ABCD in which AB = 5.1 cm, BC = 2.4 cm, CD = 6.9 cm, DA = 4.0 cm, and Diagonal AC = 6.6 cm
Solution: In this problem, the lengths of all the four sides are given. But the interior angle is missing. Instead, we are given the length of a diagonal. With these details, we can indeed draw the quadrilateral. The first step is to draw a rough sketch as shown in fig.12.24(a)
 |
| Fig.12.24 |
• Draw a horizontal line AB, 5.1 cm in length
• With A as center, draw an arc (shown in white colour in fig.b) of radius 6.6 cm. With B as center, draw an arc (shown in magenta colour in fig.b) of radius 2.4 cm
• These two arcs will intersect at C. Join B and C. So we have obtained three corners, A, B and C of the Quadrilateral. Now we have to locate the remaining corner D
• With A as center, draw an arc (shown in green colour in fig.c) of radius 4.0 cm. With C as center, draw an arc (shown in yellow colour in fig.c) of radius 6.9 cm
• These two arcs will intersect at D. Join A to D and C to D. Thus we get the required quadrilateral ABCD
Solved example 12.16
Construct a quadrilateral ABCD in which AB = 5.4 cm, BC = 4.0 cm, CD = 6.2 cm, ∠B = 105o, and ∠C = 70o
Solution: In this problem, the lengths of only three sides are given. Also no diagonal is given. Instead, two interior angles are given. With these details, we can indeed draw the quadrilateral. The first step is to draw a rough sketch as shown in fig.12.25(a)
 |
| Fig.12.25 |
• Draw line BC’ at an angle of 105o with AB
• With B as center, draw an arc (shown in magenta colour in fig.b) of radius 4 cm. This arc cuts BC’ at C. So we have obtained three corners A, B and C. We have to locate the remaining corner D
• Draw a line CD’ at an angle of 70o with BC.
• With C as center, draw an arc (shown in yellow colour in fig.c) of radius 6.2 cm. This arc cuts CD’ at D. Join A to D. Thus we get the required quadrilateral ABCD
Solved example 12.17
Construct a quadrilateral ABCD in which AB = 7.4 cm, BC = 4.3 cm, ∠A = 86o, ∠B = 47o, and ∠C = 151o
Solution: In this problem, the lengths of only three sides are given. Also no diagonal is given. Instead, two interior angles are given. With these details, we can indeed draw the quadrilateral. The first step is to draw a rough sketch as shown in fig.12.26(a)
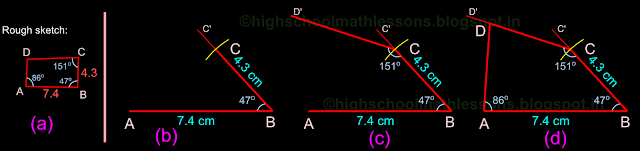 |
| Fig.12.26 |
• Draw line BC’ at an angle of 47o with AB
• With B as center, draw an arc (shown in yellow colour in fig.b) of radius 4.3 cm. This arc cuts BC’ at C. So we have obtained three corners A, B and C. We have to locate the remaining corner D
• Draw a line CD’ at an angle of 151o with BC
• Draw a line AD at an angle of 86o with AB. This line intersects CD' at D. Thus we get the required quadrilateral ABCD
Solved example 12.18
Construct a quadrilateral ABCD in which AB = 6.0 cm, BC = 5.5 cm, AD = 3.2 cm, Diagonal AC = 6.2 cm, and diagonal BD = 5.0 cm
Solution: In this problem, the lengths of three sides, and two diagonals are given. With these details, we can indeed draw the quadrilateral. The first step is to draw a rough sketch as shown in fig.12.24(a)
 |
| Fig.12.27 |
• Draw a horizontal line AB, 6.0 cm in length
• With A as center, draw an arc (shown in magenta colour in fig.b) of radius 3.2 cm. With B as center, draw an arc (shown in yellow colour in fig.b) of radius 5.0 cm
• These two arcs will intersect at D. Join A and D. So we have obtained three corners, A, B and D of the Quadrilateral. Now we have to locate the remaining corner C
• With A as center, draw an arc (shown in yellow colour in fig.c) of radius 6.2 cm. With B as center, draw an arc (shown in green colour in fig.c) of radius 5.5 cm
• These two arcs will intersect at C. Join B to C and C to D. Thus we get the required quadrilateral ABCD
So we have learned to construct a Quadrilateral under five conditions:
■ When the lengths of all the sides and one interior angle are given
■ When the lengths of all the sides and one diagonal are given
■ When the lengths of three sides and two interior angles are given
■ When the lengths of two sides and three interior angles are given
■ When the lengths of three sides and two diagonals are given
In the next section, we will learn the calculation of Areas of Quadrilaterals.
No comments:
Post a Comment