In the previous section we learned the construction of Isosceles Trapezium. In this section, we will learn the construction of Non Isosceles Trapezium.
The properties of this type of Trapezium are:
• Only one pair of opposite sides are equal. In the fig.12, there are two pairs of opposite sides: (i) [AB, CD] and (ii) [AD, BC]. Out of these two pairs, only the sides in the first pair are parallel to each other. The sides AD and BC in the second pair are Non parallel
• Non parallel sides are not equal. We have seen above that AD and BC are non parallel. These two sides are not equal in length
• Angles on each parallel sides are not equal. In the fig.(b), the parallel sides are AB and CD. Consider them separately:
♦ Consider side AB first. The angles on this side are ∠A and ∠B. These two angles are not equal. That is., ∠A ≠ ∠B.
♦ Consider side CD. The angles on this side are ∠C and ∠D. These two angles are not equal. That is., ∠C ≠ ∠D
♦ Angles on non parallel sides are also not equal. That is., ∠A ≠ ∠D and ∠B ≠ ∠C
• Sum of the angles on each non parallel sides is equal 180o. In the fig., the non parallel sides are AD and BC. Consider them separately:
♦ Consider side AD first. The angles on this side are ∠A and ∠D. Sum of these two angles is 180o. That is., ∠A + ∠D = 180o
♦ Consider side BC. The angles on this side are ∠B and ∠C. Sum of these two angles is 180o. That is., ∠C + ∠D = 180o
♦ Note that, this sum property is not applicable to angles on parallel sides
• Diagonals are not equal. AC and BD are not equal in length.
Now we will see a special feature of a Non Isosceles Trapezium:
In the previous section, we saw that, an isosceles triangle is hidden inside an isosceles trapezium. Here, in the case of non isosceles trapeziums also, a triangle is hidden. But this triangle is not an isosceles one. Let us try and find out if we can fix it's shape:
In the fig.(b), a line DE is drawn in such a way that, length of DE is equal to the length of BC. And also, DE makes the same angle ∠CBE with the base. That is.,
BC = DE - - - (1) and
∠CBE = ∠DEA - - - (2)
So the line DE splits the trapezium ABCD into a triangle AED and a parallelogram EBCD. We have thus brought out the hidden triangle. It is ΔAED. Now we have to obtain the details required to construct this ΔAED. For that, we use the properties of a parallelogram. We know that in the parallelogram EBCD, EB = CD. So AE which is equal to AB – EB can be written as AE = AB – CD. In most cases, length of CD will be given because, it is the top parallel side. So, by subtracting the top parallel side from the bottom parallel side, we get the base of the hidden triangle AED
So we have the lengths of all the three sides of the ΔAED. With those sides we can easily construct it. Once we complete the construction of ΔAED, we can easily complete the trapezium ABCD. This will become more clear when we do a solved example:
Solved example 12.9
Construct a Trapezium in which Base = 7 cm, Top parallel side = 5 cm, and the non parallel sides equal to 4 cm and 3 cm
Solution: First step is to draw a rough sketch as shown in the fig.12.17(a)
Based on the rough sketch, we can proceed to do the construction
• Draw a horizontal line AB 7 cm in length
• The base of the hidden Triangle = AE = AB – CD = 7 – 5 = 2 cm
• With A as center, draw an arc of 2 cm radius (shown in green colour in fig.b), cutting AB at E. So we obtained corners A and E of the Triangle.
• Now we want the other corner D. This D is at a distance of 4 cm from A, and 3 cm from E. So draw an arc with center A and radius 4 cm (shown in magenta colour in fig.b). Draw another arc with E as center and radius 3 cm (shown in yellow colour in fig.b).
• These two arcs will intersect at D. So we have obtained the third corner. We must now locate the remaining corner C
• DC is parallel to AB. So, through D, draw a line DC' of any convenient length, parallel to AB
• With D as center, draw an arc (shown in white colour in fig.c) of radius 5 cm, cutting DC' at C. Thus the remaining corner is also obtained. Join B to C. We get the required Trapezium ABCD
Solved example 12.10
Construct a Trapezium ABCD in which Base AB = 5 cm, Top parallel side CD = 4 cm, Non parallel side AD = 3 cm, and ∠A = 60o
Solution:
In this problem, length of one non parallel side is missing. Instead, we are given one Base angle. With those, we can indeed construct the Trapezium. The first step is to draw a rough sketch as shown in the fig. 12.18(a)
Based on the rough sketch, we can proceed to do the construction
• Draw a horizontal line AB, 5 cm in length
• Draw line AD' at an angle 60o with AB. Point D lies on this line at a distance of 3 cm from A
• With A as center, draw an arc of radius 3 cm, cutting AD' at D. This arc is shown in magenta colour in fig.(b)
• CD is parallel to AB. So draw a line DC' through C, and parallel to AB, for any convenient length
• With D as center, draw an arc (shown in green colour in fig.c) of radius 4 cm, cutting DC' at C
• Join C and B. We get the required trapezium ABCD
Solved example 12.11
Construct a Trapezium ABCD in which Base AB = 5 cm, ∠A = 60o, ∠B = 45o, and Non parallel side AD = 3 cm.
Solution:
In this problem, lengths of top parallel side CD, and one non parallel side BC, are missing. Instead, we are given two Base angles. With those, we can indeed construct the Trapezium. The first step is to draw a rough sketch as shown in the fig. 12.19(a)
Based on the rough sketch, we can proceed to do the construction
• Draw a horizontal line AB, 5 cm in length
• Draw line AD' at an angle 60o with AB. Point D lies on this line at a distance of 3 cm from A
• With A as center, draw an arc of radius 3 cm, cutting AD' at D. This arc is shown in magenta colour in fig.(b). So we get Corner D
• Draw line BC' at an angle 45o with AB. Point C lies on this line. But we do not know it's distance from B
• We know that CD is parallel to AB. So through C, draw a line CD parallel to AB.
• Extend this line until it meets the line BC' at C. Thus we get the required trapezium ABCD
Solved example 12.12
Construct a Trapezium ABCD in which Base AB = 5 cm, Top parallel side CD = 3cm, ∠A = 60o, and ∠B = 45o
Solution:
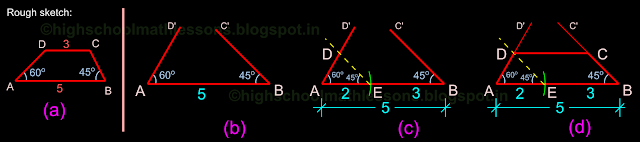
In this problem, lengths of non parallel sides BC and CA are missing. Instead, we are given the length of two parallel sides and the two Base angles. With those, we can indeed construct the Trapezium. The first step is to draw a rough sketch as shown in the fig. 12.20(a)
Based on the rough sketch, we can proceed to do the construction
• Draw a horizontal line AB, 5 cm in length
• Draw line AD' at an angle 60o with AB. Point D lies on this line. But we do not know it's distance from A
• Draw line BC' at an angle 45o with AB. Point C lies on this line. But we do not know it's distance from B
• In this problem, we have to bring out the hidden triangle AED. We know that AE = AB - CD = 5 - 3 = 2 cm
• With A as center, draw an arc or 2 cm radius, cutting AB at E. So we got the corners A and E of the hidden triangle AED. Now we have to locate the third corner D
• We know that ED will be parallel to BC. So draw a line (yellow dashed line in fig.c) parallel to BC through E
• This line intersets AD' At D. So we got all the corners of the hidden triangle. It also gives us the third corner D of the required trapezium ABCD. Now we need to locate the remaining corner C
• We know that CD is parallel to AB. So through C draw a line parallel to AB. This line will meet the line BC' at C. Thus we get the required trapezium ABCD
So we have learned to construct a Trapezium under four conditions:
■ When the lengths of all the sides are given
■ When the lengths of two parallel sides, one non parallel side, and one Base angle is given
■ When the lengths of one parallel side, one non parallel side, and two Base angles are given
■ When the lengths of two parallel sides and two Base angles are given
In the next section, we will learn the construction of Quadrilaterals of various shapes.
Construction of Non Isosceles Trapezium
A Non Isosceles Trapezium is shown in the fig.12.15 |
| Fig.12.15 |
• Only one pair of opposite sides are equal. In the fig.12, there are two pairs of opposite sides: (i) [AB, CD] and (ii) [AD, BC]. Out of these two pairs, only the sides in the first pair are parallel to each other. The sides AD and BC in the second pair are Non parallel
• Non parallel sides are not equal. We have seen above that AD and BC are non parallel. These two sides are not equal in length
• Angles on each parallel sides are not equal. In the fig.(b), the parallel sides are AB and CD. Consider them separately:
♦ Consider side AB first. The angles on this side are ∠A and ∠B. These two angles are not equal. That is., ∠A ≠ ∠B.
♦ Consider side CD. The angles on this side are ∠C and ∠D. These two angles are not equal. That is., ∠C ≠ ∠D
♦ Angles on non parallel sides are also not equal. That is., ∠A ≠ ∠D and ∠B ≠ ∠C
• Sum of the angles on each non parallel sides is equal 180o. In the fig., the non parallel sides are AD and BC. Consider them separately:
♦ Consider side AD first. The angles on this side are ∠A and ∠D. Sum of these two angles is 180o. That is., ∠A + ∠D = 180o
♦ Consider side BC. The angles on this side are ∠B and ∠C. Sum of these two angles is 180o. That is., ∠C + ∠D = 180o
♦ Note that, this sum property is not applicable to angles on parallel sides
• Diagonals are not equal. AC and BD are not equal in length.
Now we will see a special feature of a Non Isosceles Trapezium:
In the previous section, we saw that, an isosceles triangle is hidden inside an isosceles trapezium. Here, in the case of non isosceles trapeziums also, a triangle is hidden. But this triangle is not an isosceles one. Let us try and find out if we can fix it's shape:
 |
| Fig.12.16 |
BC = DE - - - (1) and
∠CBE = ∠DEA - - - (2)
So the line DE splits the trapezium ABCD into a triangle AED and a parallelogram EBCD. We have thus brought out the hidden triangle. It is ΔAED. Now we have to obtain the details required to construct this ΔAED. For that, we use the properties of a parallelogram. We know that in the parallelogram EBCD, EB = CD. So AE which is equal to AB – EB can be written as AE = AB – CD. In most cases, length of CD will be given because, it is the top parallel side. So, by subtracting the top parallel side from the bottom parallel side, we get the base of the hidden triangle AED
So we have the lengths of all the three sides of the ΔAED. With those sides we can easily construct it. Once we complete the construction of ΔAED, we can easily complete the trapezium ABCD. This will become more clear when we do a solved example:
Solved example 12.9
Construct a Trapezium in which Base = 7 cm, Top parallel side = 5 cm, and the non parallel sides equal to 4 cm and 3 cm
Solution: First step is to draw a rough sketch as shown in the fig.12.17(a)
 |
| Fig.12.17 |
• Draw a horizontal line AB 7 cm in length
• The base of the hidden Triangle = AE = AB – CD = 7 – 5 = 2 cm
• With A as center, draw an arc of 2 cm radius (shown in green colour in fig.b), cutting AB at E. So we obtained corners A and E of the Triangle.
• Now we want the other corner D. This D is at a distance of 4 cm from A, and 3 cm from E. So draw an arc with center A and radius 4 cm (shown in magenta colour in fig.b). Draw another arc with E as center and radius 3 cm (shown in yellow colour in fig.b).
• These two arcs will intersect at D. So we have obtained the third corner. We must now locate the remaining corner C
• DC is parallel to AB. So, through D, draw a line DC' of any convenient length, parallel to AB
• With D as center, draw an arc (shown in white colour in fig.c) of radius 5 cm, cutting DC' at C. Thus the remaining corner is also obtained. Join B to C. We get the required Trapezium ABCD
Solved example 12.10
Construct a Trapezium ABCD in which Base AB = 5 cm, Top parallel side CD = 4 cm, Non parallel side AD = 3 cm, and ∠A = 60o
Solution:
In this problem, length of one non parallel side is missing. Instead, we are given one Base angle. With those, we can indeed construct the Trapezium. The first step is to draw a rough sketch as shown in the fig. 12.18(a)
 |
| Fig.12.18 |
• Draw a horizontal line AB, 5 cm in length
• Draw line AD' at an angle 60o with AB. Point D lies on this line at a distance of 3 cm from A
• With A as center, draw an arc of radius 3 cm, cutting AD' at D. This arc is shown in magenta colour in fig.(b)
• CD is parallel to AB. So draw a line DC' through C, and parallel to AB, for any convenient length
• With D as center, draw an arc (shown in green colour in fig.c) of radius 4 cm, cutting DC' at C
• Join C and B. We get the required trapezium ABCD
Solved example 12.11
Construct a Trapezium ABCD in which Base AB = 5 cm, ∠A = 60o, ∠B = 45o, and Non parallel side AD = 3 cm.
Solution:
In this problem, lengths of top parallel side CD, and one non parallel side BC, are missing. Instead, we are given two Base angles. With those, we can indeed construct the Trapezium. The first step is to draw a rough sketch as shown in the fig. 12.19(a)
 |
| Fig.12.19 |
• Draw a horizontal line AB, 5 cm in length
• Draw line AD' at an angle 60o with AB. Point D lies on this line at a distance of 3 cm from A
• With A as center, draw an arc of radius 3 cm, cutting AD' at D. This arc is shown in magenta colour in fig.(b). So we get Corner D
• Draw line BC' at an angle 45o with AB. Point C lies on this line. But we do not know it's distance from B
• We know that CD is parallel to AB. So through C, draw a line CD parallel to AB.
• Extend this line until it meets the line BC' at C. Thus we get the required trapezium ABCD
Solved example 12.12
Construct a Trapezium ABCD in which Base AB = 5 cm, Top parallel side CD = 3cm, ∠A = 60o, and ∠B = 45o
Solution:
In this problem, lengths of non parallel sides BC and CA are missing. Instead, we are given the length of two parallel sides and the two Base angles. With those, we can indeed construct the Trapezium. The first step is to draw a rough sketch as shown in the fig. 12.20(a)
 |
| Fig.12.20 |
• Draw a horizontal line AB, 5 cm in length
• Draw line AD' at an angle 60o with AB. Point D lies on this line. But we do not know it's distance from A
• Draw line BC' at an angle 45o with AB. Point C lies on this line. But we do not know it's distance from B
• In this problem, we have to bring out the hidden triangle AED. We know that AE = AB - CD = 5 - 3 = 2 cm
• With A as center, draw an arc or 2 cm radius, cutting AB at E. So we got the corners A and E of the hidden triangle AED. Now we have to locate the third corner D
• We know that ED will be parallel to BC. So draw a line (yellow dashed line in fig.c) parallel to BC through E
• This line intersets AD' At D. So we got all the corners of the hidden triangle. It also gives us the third corner D of the required trapezium ABCD. Now we need to locate the remaining corner C
• We know that CD is parallel to AB. So through C draw a line parallel to AB. This line will meet the line BC' at C. Thus we get the required trapezium ABCD
So we have learned to construct a Trapezium under four conditions:
■ When the lengths of all the sides are given
■ When the lengths of two parallel sides, one non parallel side, and one Base angle is given
■ When the lengths of one parallel side, one non parallel side, and two Base angles are given
■ When the lengths of two parallel sides and two Base angles are given
In the next section, we will learn the construction of Quadrilaterals of various shapes.
No comments:
Post a Comment