In the previous section we saw Step deviation method. We also saw some solved examples demonstrating all three methods. In this section we will see a few more solved examples.
Solved example 37.2
Consider the following distribution of daily wages of 50 workers of a factory.
Find the mean daily wages of the workers of the factory by using an appropriate method.
Solution:
• We will try all the three methods and then decide which method is appropriate. This will help us to select a method when we encounter such problems in the future. The three methods are:
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.15
• a is taken as 150, since it is the middle xi
• h is taken as 20, since it is the class width
1. Direct method:
• x is given by the formula:
• The numerator is calculated at the bottom end of the sixth column. It's value is 7260
• The denominator is calculated at the bottom end of second column. It's value is 50
• So we get x = 7260⁄50 = 145.2
2. Assumed mean method:
• d is given by the formula:
• The numerator is calculated at the bottom end of the seventh column. It's value is -240
• The denominator is calculated at the bottom end of second column. It's value is 50
• So we get d = -240⁄50 = - 4.8
• Thus x = a + d = 150 - 4.8 = 145.2
■ This is the same value obtained by method 1
3. Step deviation method:
• u is given by the formula:
• The numerator is calculated at the bottom end of the eighth column. It's value is -12
• The denominator is calculated at the bottom end of second column. It's value is 50
• So we get u = -12⁄50 = - 0.24
• Thus x = a + hu = 150 + (20 × -0.24) = 150 - 4.8 = 145.2
■ This is the same value obtained by methods 1 & 2
■ In this problem, the values in the xi column are not small. They are hundreds
• Because of these high values, we get thousands in the sixth column. It is not convenient to find all those thousands and then do calculations with them.
• So we must reduce xi by subtracting 'a' from it. Thus we get di. But then, we get hundreds in the seventh column. It is not convenient to deal with hundreds either
• So we must reduce di by dividing it with 'h'. We get small numbers in the eighth column
■ Upon seeing hundreds in the xi column, we can immediately decide to use the step deviation method. We need not fill up the sixth and seventh columns
■ The significance of the result is clear in this problem:
The average (or mean) wages of workers in that factory is 145.2 per day
• The factory owner has to deal with two items: Daily Income and Daily Expense
• Under Daily expense, he has two items:
♦ Total cost of material per day
♦ Total cost of labour per day
• There are 50 workers. So the 'total cost of labour per day' will be approximately equal to (50×145.2) = 7260
• To obtain accurate values, we will have to apply more advanced principles of statistics. We will see them in higher classes
Solved example 37.3
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f.
Solution:
• We will try all the three methods and then decide which method is appropriate. This will help us to select a method when we encounter such problems in the future. The three methods are:
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.17
• a is taken as 18, since it is the middle xi
• h is taken as 2, since it is the class width
1. Direct method:
• x is given by the formula:
• The numerator is calculated at the bottom end of the sixth column. It's value is (752+20f)
• The denominator is calculated at the bottom end of second column. It's value is (44+f)
• So we get x = (752+20f)⁄(44+f)
• But this mean is given to us as 18. So we can write:
(752+20f)⁄(44+f) = 18 ⟹ (752+20f) = 18(44+f) ⟹ (752+20f) = (792+18f) ⟹ 2f = 40 ⟹ f = 20
2. Assumed mean method:
• d is given by the formula:
• The numerator is calculated at the bottom end of the seventh column. It's value is (-40+2f)
• The denominator is calculated at the bottom end of second column. It's value is (44+f)
• So we get d = (-40+2f)⁄(44+f)
• Thus x = a + d = [18 + (-40+2f)⁄(44+f)]
• But this mean is given to us as 18. So we can write:
[18 + (-40+2f)⁄(44+f)] = 18 ⟹ [(-40+2f)⁄(44+f)] = 0 ⟹ (-40+2f) = 0 ⟹ 2f = 40 ⟹ f = 20
■ This is the same value obtained by method 1
3. Step deviation method:
• u is given by the formula:
• The numerator is calculated at the bottom end of the eighth column. It's value is (-20+f)
• The denominator is calculated at the bottom end of second column. It's value is (44+f)
• So we get u = (-20+f)⁄(44+f)
• Thus x = a + hu = [18 + (2 × (-20+f)⁄(44+f))]
• But this mean is given to us as 18. So we can write:
[18 + (2 × (-20+f)⁄(44+f))] = 18 ⟹ [(2 × (-20+f)⁄(44+f))] = 0 ⟹ [(-20+f)⁄(44+f)] = 0
⟹ (-20+f) = 0 ⟹ f = 20
■ This is the same value obtained by methods 1 & 2
■ In this problem, the step deviation method is appropriate because, as we see in the eighth column, it is easier to do calculations with small numbers. So there is no need to fill up the sixth and seventh columns.
Solved example 37.4
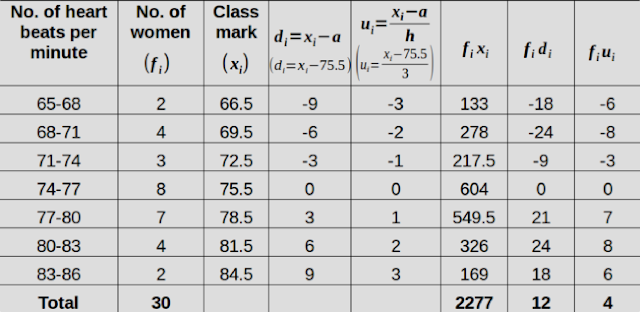
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute were recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method.
Solution:
• We will try all the three methods and then decide which method is appropriate. This will help us to select a method when we encounter such problems in the future. The three methods are:
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.19
• a is taken as 75.5, since it is the middle xi
• h is taken as 3, since it is the class width
1. Direct method:
• x is given by the formula:
• The numerator is calculated at the bottom end of the sixth column. It's value is 2277
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get x = 2277⁄30 = 75.9
2. Assumed mean method:
• d is given by the formula:
• The numerator is calculated at the bottom end of the seventh column. It's value is 12
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get d = 12⁄30 = 0.4
• Thus x = a + d = 75.5 + 0.4 = 75.9
■ This is the same value obtained by method 1
3. Step deviation method:
• u is given by the formula:
• The numerator is calculated at the bottom end of the eighth column. It's value is 4
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get u = 4⁄30
• Thus x = a + hu = [75.5 + (3 × 4⁄30)] = 75.9
■ This is the same value obtained by methods 1 & 2
■ In this problem, the step deviation method is appropriate because, as we see in the eighth column, it is easier to do calculations with small numbers. So there is no need to fill up the sixth and seventh columns.
Solved example 37.5
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.
Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
Solution:
• The class intervals given to us are not continuous. There is a gap of '1' between all the class intervals
♦ For example, the gap between the first and second intervals is (53-52) = 1
• We know the method to make the intervals continuous. (Details here)
• The new table 37.21 is given below:
• Now we can begin to solve the problem. We will try all the three methods and then decide which method is appropriate. This will help us to select a method when we encounter such problems in the future. The three methods are:
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.22
• a is taken as 57, since it is the middle xi
• h is taken as 3, since it is the class width
1. Direct method:
• x is given by the formula:
• The numerator is calculated at the bottom end of the sixth column. It's value is 22875
• The denominator is calculated at the bottom end of second column. It's value is 400
• So we get x = 22875⁄400 = 57.1875
2. Assumed mean method:
• d is given by the formula:
• The numerator is calculated at the bottom end of the seventh column. It's value is 12
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get d = 75⁄400 = 0.1875
• Thus x = a + d = 57 + 0.1875 = 57.1875
■ This is the same value obtained by method 1
3. Step deviation method:
• u is given by the formula:
• The numerator is calculated at the bottom end of the eighth column. It's value is 4
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get u = 25⁄400
• Thus x = a + hu = [57 + (3 × 25⁄400)] = 57.1875
■ This is the same value obtained by methods 1 & 2
■ In this problem, the step deviation method is appropriate because, as we see in the eighth column, it is easier to do calculations with small numbers. So there is no need to fill up the sixth and seventh columns.
Solved example 37.6
The mean of the following distribution is 50. Also Σf = 120. Find the missing frequencies f1 and f2.
Solution:
• We will try all the three methods and then decide which method is appropriate. This will help us to select a method when we encounter such problems in the future. The three methods are:
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.24
• a is taken as 50, since it is the middle xi
• h is taken as 20, since it is the class width
• From the table, it is clear that, the step deviation method is appropriate because, it involves smaller numbers in the eighth column. So we will use it:
Step deviation method:
• u is given by the formula:
• The numerator will be the value at the bottom end of the sixth column. It is (4-f1+f2)
• The denominator will be the value at the bottom end of the second column. It is (68+f1+f2)
• So we get u = (4-f1+f2)⁄(68+f1+f2)
• Thus x = a + hu = [50 + (20 × (4-f1+f2)⁄(68+f1+f2))]
• But this mean is given to us as 50. So we can write:
[50 + (20 × (4-f1+f2)⁄(68+f1+f2))] = 50 ⟹ [(20 × (4-f1+f2)⁄(68+f1+f2))] = 0
⟹ (4-f1+f2)⁄(68+f1+f2) = 0 ⟹ (4-f1+f2) = 0 ⟹ f1- f2 = 4
• Now consider the denominator. In the denominator, there will be Σf. But Σf is given as 120
So we can write: Σf = (68+f1+f2) = 120 ⟹ (f1+f2) = 52
• Thus we have two equations:
(i) f1 + f2 = 52
(ii) f1 - f2 = 4
• From (ii) we get: f2 = (f1-4)
• substituting this in (i), we get:
f1 + f1 - 4 = 52 ⟹ 2f1 = 56 ⟹ f1 = 28
• Substituting this value of f1 in (ii) we get:
f2 = 28 - 4 = 24
In the next section, we will discuss about mode.
Solved example 37.2
Consider the following distribution of daily wages of 50 workers of a factory.
 |
| Table.37.14 |
Solution:
• We will try all the three methods and then decide which method is appropriate. This will help us to select a method when we encounter such problems in the future. The three methods are:
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.15
• a is taken as 150, since it is the middle xi
• h is taken as 20, since it is the class width
 |
| Table.37.15 |
• x is given by the formula:
• The numerator is calculated at the bottom end of the sixth column. It's value is 7260
• The denominator is calculated at the bottom end of second column. It's value is 50
• So we get x = 7260⁄50 = 145.2
2. Assumed mean method:
• d is given by the formula:
• The denominator is calculated at the bottom end of second column. It's value is 50
• So we get d = -240⁄50 = - 4.8
• Thus x = a + d = 150 - 4.8 = 145.2
■ This is the same value obtained by method 1
3. Step deviation method:
• u is given by the formula:
• The denominator is calculated at the bottom end of second column. It's value is 50
• So we get u = -12⁄50 = - 0.24
• Thus x = a + hu = 150 + (20 × -0.24) = 150 - 4.8 = 145.2
■ This is the same value obtained by methods 1 & 2
■ In this problem, the values in the xi column are not small. They are hundreds
• Because of these high values, we get thousands in the sixth column. It is not convenient to find all those thousands and then do calculations with them.
• So we must reduce xi by subtracting 'a' from it. Thus we get di. But then, we get hundreds in the seventh column. It is not convenient to deal with hundreds either
• So we must reduce di by dividing it with 'h'. We get small numbers in the eighth column
■ Upon seeing hundreds in the xi column, we can immediately decide to use the step deviation method. We need not fill up the sixth and seventh columns
■ The significance of the result is clear in this problem:
The average (or mean) wages of workers in that factory is 145.2 per day
• The factory owner has to deal with two items: Daily Income and Daily Expense
• Under Daily expense, he has two items:
♦ Total cost of material per day
♦ Total cost of labour per day
• There are 50 workers. So the 'total cost of labour per day' will be approximately equal to (50×145.2) = 7260
• To obtain accurate values, we will have to apply more advanced principles of statistics. We will see them in higher classes
Solved example 37.3
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f.
 |
| Table.37.16 |
• We will try all the three methods and then decide which method is appropriate. This will help us to select a method when we encounter such problems in the future. The three methods are:
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.17
• a is taken as 18, since it is the middle xi
• h is taken as 2, since it is the class width
 |
| Table.37.17 |
• x is given by the formula:
• The numerator is calculated at the bottom end of the sixth column. It's value is (752+20f)
• The denominator is calculated at the bottom end of second column. It's value is (44+f)
• So we get x = (752+20f)⁄(44+f)
• But this mean is given to us as 18. So we can write:
(752+20f)⁄(44+f) = 18 ⟹ (752+20f) = 18(44+f) ⟹ (752+20f) = (792+18f) ⟹ 2f = 40 ⟹ f = 20
2. Assumed mean method:
• d is given by the formula:
• The denominator is calculated at the bottom end of second column. It's value is (44+f)
• So we get d = (-40+2f)⁄(44+f)
• Thus x = a + d = [18 + (-40+2f)⁄(44+f)]
• But this mean is given to us as 18. So we can write:
[18 + (-40+2f)⁄(44+f)] = 18 ⟹ [(-40+2f)⁄(44+f)] = 0 ⟹ (-40+2f) = 0 ⟹ 2f = 40 ⟹ f = 20
■ This is the same value obtained by method 1
3. Step deviation method:
• u is given by the formula:
• The denominator is calculated at the bottom end of second column. It's value is (44+f)
• So we get u = (-20+f)⁄(44+f)
• Thus x = a + hu = [18 + (2 × (-20+f)⁄(44+f))]
• But this mean is given to us as 18. So we can write:
[18 + (2 × (-20+f)⁄(44+f))] = 18 ⟹ [(2 × (-20+f)⁄(44+f))] = 0 ⟹ [(-20+f)⁄(44+f)] = 0
⟹ (-20+f) = 0 ⟹ f = 20
■ This is the same value obtained by methods 1 & 2
■ In this problem, the step deviation method is appropriate because, as we see in the eighth column, it is easier to do calculations with small numbers. So there is no need to fill up the sixth and seventh columns.
Solved example 37.4
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute were recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method.
 |
| Table.37.18 |
• We will try all the three methods and then decide which method is appropriate. This will help us to select a method when we encounter such problems in the future. The three methods are:
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.19
• a is taken as 75.5, since it is the middle xi
• h is taken as 3, since it is the class width
 |
| Table.37.19 |
• x is given by the formula:
• The numerator is calculated at the bottom end of the sixth column. It's value is 2277
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get x = 2277⁄30 = 75.9
2. Assumed mean method:
• d is given by the formula:
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get d = 12⁄30 = 0.4
• Thus x = a + d = 75.5 + 0.4 = 75.9
■ This is the same value obtained by method 1
3. Step deviation method:
• u is given by the formula:
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get u = 4⁄30
• Thus x = a + hu = [75.5 + (3 × 4⁄30)] = 75.9
■ This is the same value obtained by methods 1 & 2
■ In this problem, the step deviation method is appropriate because, as we see in the eighth column, it is easier to do calculations with small numbers. So there is no need to fill up the sixth and seventh columns.
Solved example 37.5
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.
 |
| Table.37.20 |
• The class intervals given to us are not continuous. There is a gap of '1' between all the class intervals
♦ For example, the gap between the first and second intervals is (53-52) = 1
• We know the method to make the intervals continuous. (Details here)
• The new table 37.21 is given below:
 |
| Table.37.21 |
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.22
• a is taken as 57, since it is the middle xi
• h is taken as 3, since it is the class width
 |
| Table.37.22 |
• x is given by the formula:
• The numerator is calculated at the bottom end of the sixth column. It's value is 22875
• The denominator is calculated at the bottom end of second column. It's value is 400
• So we get x = 22875⁄400 = 57.1875
2. Assumed mean method:
• d is given by the formula:
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get d = 75⁄400 = 0.1875
• Thus x = a + d = 57 + 0.1875 = 57.1875
■ This is the same value obtained by method 1
3. Step deviation method:
• u is given by the formula:
• The denominator is calculated at the bottom end of second column. It's value is 30
• So we get u = 25⁄400
• Thus x = a + hu = [57 + (3 × 25⁄400)] = 57.1875
■ This is the same value obtained by methods 1 & 2
■ In this problem, the step deviation method is appropriate because, as we see in the eighth column, it is easier to do calculations with small numbers. So there is no need to fill up the sixth and seventh columns.
Solved example 37.6
The mean of the following distribution is 50. Also Σf = 120. Find the missing frequencies f1 and f2.
 |
| Table.37.23 |
• We will try all the three methods and then decide which method is appropriate. This will help us to select a method when we encounter such problems in the future. The three methods are:
(i) Direct method, (ii) Assumed mean method and (iii) Step deviation method
♦ Method (i) has Σfixi in the numerator
♦ Method (ii) has Σfidi in the numerator
♦ Method (iii) has Σfiui in the numerator
• All the three numerators can be conveniently calculated in a single table. It is shown below as table 37.24
• a is taken as 50, since it is the middle xi
• h is taken as 20, since it is the class width
 |
| Table.37.24 |
Step deviation method:
• u is given by the formula:
• The denominator will be the value at the bottom end of the second column. It is (68+f1+f2)
• So we get u = (4-f1+f2)⁄(68+f1+f2)
• Thus x = a + hu = [50 + (20 × (4-f1+f2)⁄(68+f1+f2))]
• But this mean is given to us as 50. So we can write:
[50 + (20 × (4-f1+f2)⁄(68+f1+f2))] = 50 ⟹ [(20 × (4-f1+f2)⁄(68+f1+f2))] = 0
⟹ (4-f1+f2)⁄(68+f1+f2) = 0 ⟹ (4-f1+f2) = 0 ⟹ f1- f2 = 4
• Now consider the denominator. In the denominator, there will be Σf. But Σf is given as 120
So we can write: Σf = (68+f1+f2) = 120 ⟹ (f1+f2) = 52
• Thus we have two equations:
(i) f1 + f2 = 52
(ii) f1 - f2 = 4
• From (ii) we get: f2 = (f1-4)
• substituting this in (i), we get:
f1 + f1 - 4 = 52 ⟹ 2f1 = 56 ⟹ f1 = 28
• Substituting this value of f1 in (ii) we get:
f2 = 28 - 4 = 24



No comments:
Post a Comment